题目内容
12.函数y=$\frac{1}{\sqrt{{x}^{2}-2x-3}}$的单调递减区间是(3,+∞).分析 根据复合函数单调性之间的关系进行求解即可.
解答 解:由x2-2x-3>0得x>3或x<-1,
设t=x2-2x-3,则y=$\frac{1}{\sqrt{t}}$为减函数,
∴要求函数y=$\frac{1}{\sqrt{{x}^{2}-2x-3}}$的单调递减区间,
即求t=x2-2x-3的单调递增区间,
∵t=x2-2x-3的单调递增区间是(3,+∞),
∴y=$\frac{1}{\sqrt{{x}^{2}-2x-3}}$的单调递减区间是(3,+∞),
故答案为:(3,+∞).
点评 本题主要考查函数单调区间的求解,根据复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
20.若f(x)是定义在R上的偶函数,且满足f(x)=-f(x+$\frac{3}{2}$),f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2008)的值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
1.函数y=$\frac{{x}^{2}+2x+6}{x-1}$(x>1)的最小值为( )
| A. | 10 | B. | 9 | C. | 6 | D. | 4 |
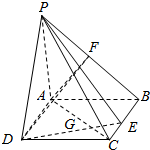 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD=$\sqrt{3}$,E、F、G分别是BC、PB、AD上的点,且AF⊥PC,AG=3GD.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD=$\sqrt{3}$,E、F、G分别是BC、PB、AD上的点,且AF⊥PC,AG=3GD.