题目内容
17.在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(3,0)的值为( )| A. | 4 | B. | 10 | C. | 20 | D. | 40 |
分析 由条件利用二项展开式的通项公式求得含x3y0的系数,即f(3,0)的值.
解答 解:∵(1+x)6(1+y)4的展开式中,含x3y0的系数是:f(3,0)=${C}_{6}^{3}$=20,
故选:C.
点评 本题考查二项式定理的应用,二项展开式的通项公式,考查计算能力,属于基础题.

练习册系列答案
相关题目
7.下列函数中,既是偶函数又在(0,+∞)上是单调递增函数的是( )
| A. | y=lgx | B. | y=-x2+3 | C. | y=|x|-1 | D. | y=3x |
12.阅读以下程序:

若输出y=16,则输入的x值应该是( )

若输出y=16,则输入的x值应该是( )
| A. | 3或-3 | B. | -5或5 | C. | 5或-3 | D. | -5 |
2.在等差数列{an}中,已知a2+a3+a4=18,那么s5=( )
| A. | 30 | B. | 35 | C. | 18 | D. | 26 |
9.等差数列{an}的前n项和为Sn,已知a1=-12,S13=0,使得an>0的最小正整数n等于( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
 (
( 为常数,
为常数,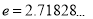 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与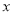 轴平行.
轴平行.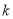 的值;
的值; 的单调区间;
的单调区间; ,其中
,其中 为
为 的导函数.证明:对任意
的导函数.证明:对任意 ,
,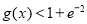 .
.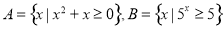 ,则
,则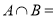 ( )
( )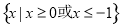 B.
B.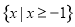
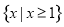 D.
D.