题目内容
【题目】已知函数f（x）＝|sinx||cosx|，则下列说法正确的是（ ）
A.f（x）的图象关于直线
对称
B.f（x）的周期为
C.（π，0）是f（x）的一个对称中心
D.f（x）在区间
上单调递增
【答案】AB
【解析】
先根据二倍角公式化简变形函数f（x），再作出其图象，即可判断各选项的真假．
因为函数f（x）＝|sinx||cosx|＝|sinxcosx|
|sin2x|，
画出函数图象，如图所示；
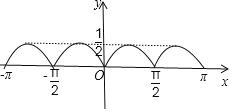
由图可知，f（x）的对称轴是x
，k∈Z；
所以x
是f（x）图象的一条对称轴， A正确；
f（x）的最小正周期是
，所以B正确；
f（x）是偶函数，没有对称中心，C错误；
由图可知，f（x）|sin2x|在区间
上是单调减函数，D错误.
故选：AB.
练习册系列答案
相关题目
