题目内容
【题目】已知圆![]() 的方程为
的方程为![]() ,若抛物线
,若抛物线![]() 过点
过点![]() ,且以圆0的切线为准线,
,且以圆0的切线为准线,![]() 为抛物线的焦点,点
为抛物线的焦点,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交曲线
交曲线![]() 与
与![]() 两点,
两点,![]() 关于
关于![]() 轴对称,请问:直线
轴对称,请问:直线![]() 是否过
是否过![]() 轴上的定点,如果不过请说明理由,如果过定点,请求出定点
轴上的定点,如果不过请说明理由,如果过定点,请求出定点![]() 的坐标
的坐标
【答案】(1)![]() (2)直线
(2)直线![]() 过
过![]() 轴上的定点
轴上的定点![]()
【解析】分析:设直线![]() 和圆
和圆![]() 相切与点
相切与点![]() ,过
,过![]() 分别向直线m作垂线,垂足分别为
分别向直线m作垂线,垂足分别为![]() ,则
,则
![]() ,由抛物线定义可知,
,由抛物线定义可知,![]() ,所以
,所以![]() ,由椭圆的定义可知,点F的轨迹为以
,由椭圆的定义可知,点F的轨迹为以![]() 为焦点,以4为长轴的椭圆,则曲线
为焦点,以4为长轴的椭圆,则曲线![]() 的方程可求;
的方程可求;
(2)设![]() ,则
,则![]() 直线
直线![]() 的方程为
的方程为![]()
令y=0,![]() ,
,
设直线L:![]() ,
,
则![]() (*) 联立直线和椭圆方程
(*) 联立直线和椭圆方程![]() ,
,
可得![]() 的表达式,代入(*)式得:
的表达式,代入(*)式得:![]() ,即可证明直线
,即可证明直线![]() 过
过![]() 轴上的定点
轴上的定点![]() .
.
详解:
(1)设直线![]() 和圆
和圆![]() 相切与点
相切与点![]() ,过
,过![]() 分别向直线m作垂线,垂足分别为
分别向直线m作垂线,垂足分别为![]() ,则
,则
![]() ,由抛物线定义可知,
,由抛物线定义可知,![]() ,所以
,所以![]() ,由椭圆的定义可知,点F的轨迹为以
,由椭圆的定义可知,点F的轨迹为以![]() 为焦点,以4为长轴的椭圆,方程为
为焦点,以4为长轴的椭圆,方程为![]() .
.
(2)设![]() ,则
,则![]() 直线
直线![]() 的方程为
的方程为![]()
令y=0,![]() ,
,
设直线L:![]() ,
,
则![]() (*) 联立直线和椭圆方程
(*) 联立直线和椭圆方程![]() ,
,
则![]() ,代入(*)式得:
,代入(*)式得:![]() ,所以直线
,所以直线![]() 过
过![]() 轴上的定点
轴上的定点![]() .
.

练习册系列答案
相关题目
【题目】手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 45 | 75 | 90 | 60 | 30 |
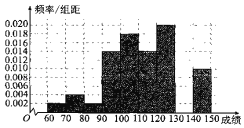
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);

(2)把评分不低于70分的用户称为“评分良好用户”,能否有![]() 的把握认为“评分良好用户”与性别有关?
的把握认为“评分良好用户”与性别有关?
参考附表:
|
|
|
| |
|
|
|
|
|
参考公式 ,其中
,其中![]()