题目内容
【题目】某中学高一期中考试结束后,从高一年级1000名学生中任意抽取50名学生,将这50名学生的某一科的考试成绩(满分150分)作为样本进行统计,并作出样本成绩的频率分布直方图(如图).
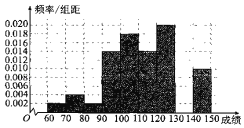
(1)由于工作疏忽,将成绩[130,140)的数据丢失,求此区间的人数及频率分布直方图的中位数;(结果保留两位小数)
(2)若规定考试分数不小于120分为优秀,现从样本的优秀学生中任意选出3名学生,参加学习经验交流会.设X表示参加学习经验交流会的学生分数不小于130分的学生人数,求X的分布列及期望;
(3)视样本频率为概率.由于特殊原因,有一个学生不能到学校参加考试,根据以往考试成绩,一般这名学生的成绩应在平均分左右.试根据以上数据,说明他若参加考试,可能得多少分?(每组数据以区问的中点值为代表)
【答案】(1)8, 117.14;(2)见解析;(3)115.4
【解析】
(1)先求出这50名学生成绩在各区间的频率及人数,由此能求出![]() ,
,![]() 的频率为0.16,人数为8,从而能求出中位数.(2)考试分数不小于120分的优秀学生有23人,
的频率为0.16,人数为8,从而能求出中位数.(2)考试分数不小于120分的优秀学生有23人,![]() 表示参加教学交流会的不小于130分的学生人数的取值为0,1,2,3,分别求出相应的概率,由此能求出
表示参加教学交流会的不小于130分的学生人数的取值为0,1,2,3,分别求出相应的概率,由此能求出![]() 的分布列和
的分布列和![]() .(3)利用频率分布直方图能求出平均分.
.(3)利用频率分布直方图能求出平均分.
(1)这50名学生成绩在各区间的频率及人数如下:[60,70)的频率为0.02,人数为1,
[70,80)的频率为0.04,人数为2,[80,90)的频率为0.02,人数为1,
[90,100)的频率为0.14,人数为7,[100,110)的频率为0.18,人数为9,
[110,120)的频率为0.14,人数为7,[120,130)的频率为0.2,人数为10,
[140,150)的频率为0.1,人数为5,∴[130,140)的频率为0.16,人数为8,
∵中位数把频率分布直方图分成左右面积相等,设中位数为m,[60,110)的频率和为:
0.02+0.04+0.02+0.14+0.18=0.4,[110,120)的频率为0.14,
∴(m﹣110)×0.14=0.5﹣0.4=0.1,解得m=![]() ≈117.14.
≈117.14.
所以频率分布直方图的中位数为117.14.
(2)考试分数不小于120分的优秀学生有23人,X表示参加教学交流会的不小于130分的学生人数的取值为0,1,2,3,
P(X=0)=![]() ,
,
P(X=1)=![]() ,
,
P(X=2)=![]() ,
,
P(X=3)![]() ,
,
∴X的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
E(X)![]() ;
;
(3)平均分W=65×0.02+75×0.04+85×0.02+95×0.14+105×0.18+115×0.14+125×0.2+135×0.16+145×0.1=115.4,
∴该学生可能得分为115.4分.