题目内容
【题目】已知数列{an}是无穷数列,满足lgan+1=|lgan﹣lgan﹣1|(n=2,3,4,…).
(1)若a1=2,a2=3,求a3 , a4 , a5的值;
(2)求证:“数列{an}中存在ak(k∈N*)使得lgak=0”是“数列{an}中有无数多项是1”的充要条件;
(3)求证:在数列{an}中ak(k∈N*),使得1≤ak<2.
【答案】
(1)解:∵a1=2,a2=3,lgan+1=|lgan﹣lgan﹣1|(n=2,3,4,…),
∴lga3=|lg3﹣lg2|= ![]() ,即
,即 ![]() ;
;
![]() ,即a4=2;
,即a4=2;
![]() ,即
,即 ![]() ;
;
(2)证明:必要性、已知数列{an}中有无数多项是1,则数列{an}中存在ak(k∈N*)使得lgak=0.
∵数列{an}中有无数多项是1,∴数列{an}中存在ak(k∈N*)使得ak=1,
即数列{an}中存在ak(k∈N*)使得lgak=0.
充分性:已知数列{an}中存在ak(k∈N*)使得lgak=0,则数列{an}中有无数多项是1.
假设数列{an}中没有无数多项是1,不妨设 ![]() 是数列{an}中为1的最后一项,则am+1≠1,
是数列{an}中为1的最后一项,则am+1≠1,
若am+1>1,则由lgan+1=|lgan﹣lgan﹣1|(n=2,3,4,…),可得lgam+2=lgam+1,
∴lgam+3=|lgam+2﹣lgam+1|=0,则lgam+3=1,与假设矛盾;
若0<am+1<0,则由lgan+1=|lgan﹣lgan﹣1|(n=2,3,4,…),可得lgam+2=﹣lgam+1,
∴lgam+3=|lgam+2﹣lgam+1|=﹣2lgam+1,
lgam+4=|lgam+3﹣lgam+2|=|﹣2lgam+1+lgam+1|=﹣lgam+1,
lgam+5=|lgam+4﹣lgam+3|=|﹣lgam+1+2lgam+1|=﹣lgam+1,
∴lgam+6=|lgam+5﹣lgam+4|=0,得lgam+6=1,与假设矛盾.
综上,假设不成立,原命题正确;
(3)证明:假设数列{an}中不存在ak(k∈N*),使得1≤ak<2,
则0<ak<1或ak≥2(k=1,2,3,…).
由lgan+1=|lgan﹣lgan﹣1|(n=2,3,4,…),可得
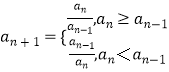 (n=1,2,3,…)*,且an>0(n=1,2,3,…),
(n=1,2,3,…)*,且an>0(n=1,2,3,…),
∴当n≥2时,an≥1,an≥2(n=3,4,5,…).
若a4=a3≥2,则a5=1,与a5≥2矛盾;
若a4≠a3≥2,
设bm=max{a2m+1,a2m+2}(m=1,2,3,…),则bm≥2.
由(*)可得, ![]() ,
,
![]() ,
,
∴ ![]() ,即
,即 ![]() (m=1,2,3,…),
(m=1,2,3,…),
∴ ![]() ,
,
对于b1,显然存在l使得 ![]() .
.
∴ ![]() ,这与bm≥2矛盾.
,这与bm≥2矛盾.
∴假设不成立,原命题正确
【解析】(1)由a1=2,a2=3,结合lgan+1=|lgan﹣lgan﹣1|(n=2,3,4,…)可得a3 , a4 , a5的值;(2)分必要性和充分性证明,充分性利用反证法证明;(3)利用反证法,假设数列{an}中不存在ak(k∈N*),使得1≤ak<2,则0<ak<1或ak≥2(k=1,2,3,…).然后分类推出矛盾得答案.
【考点精析】关于本题考查的数列的通项公式,需要了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.