题目内容
已知二次函数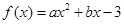 在
在 处取得极值,且在
处取得极值,且在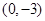 点处的切线与直线
点处的切线与直线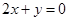 平行.
平行.
(1)求 的解析式;
的解析式;
(2)求函数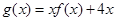 的单调递增区间及极值。
的单调递增区间及极值。
(3)求函数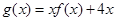 在
在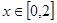 的最值。
的最值。
(1)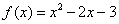 (2)函数g(x)的单调递增区间为(﹣∞,
(2)函数g(x)的单调递增区间为(﹣∞, ),(1,+∞).在x2=1有极小值为0.在
),(1,+∞).在x2=1有极小值为0.在 有极大值
有极大值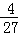 .(3)函数g(x)的最大值为2,最小值为0.
.(3)函数g(x)的最大值为2,最小值为0.
解析试题分析:(1)由f(x)=ax2+bx﹣3,知f′(x)=2ax+b.由二次函数f(x)=ax2+bx﹣3在x=1处取得极值,且在(0,﹣3)点处的切线与直线2x+y=0平行,知 ,由此能求出f(x).
,由此能求出f(x).
(2)由f(x)=x2﹣2x﹣3,知g(x)=xf(x)+4x=x3﹣2x2+x,所以g′(x)=3x2﹣4x+1=(3x﹣1)(x﹣1).令g′(x)=0,得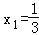 ,x2=1.列表讨论能求出函数g(x)=xf(x)+4x的单调递增区间及极值.
,x2=1.列表讨论能求出函数g(x)=xf(x)+4x的单调递增区间及极值.
(3)由g(0)=0,g(2)=2,结合(2)的结论,能求出函数g(x)的最大值和最小值.
试题解析:(1)由 ,可得
,可得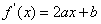 . 由题设可得
. 由题设可得 即
即
解得 ,
,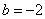 .所以
.所以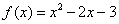 .
.
(2)由题意得 ,所以
,所以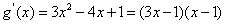 .令
.令 ,得
,得 ,
,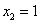 .
. 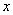
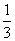
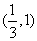
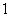
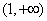
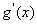
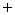

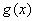
4/27 
新浪书业复习总动员学期总复习寒系列答案

自主假期作业本吉林大学出版社系列答案
高中新课程寒假作业系列答案
海淀黄冈寒假作业合肥工业大学出版社系列答案
寒假Happy假日系列答案
寒假成长乐园系列答案

寒假创新性自主学习寒假突破系列答案
寒假高效作业系列答案
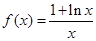 .
.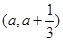
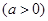 上存在极值点,求实数a的取值范围;
上存在极值点,求实数a的取值范围; 时,不等式
时,不等式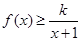 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;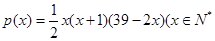 ,且
,且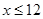 )。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
)。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
 。
。 对任意的
对任意的 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。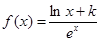 (k为常数,e=2.71828…是自然对数的底数),曲线
(k为常数,e=2.71828…是自然对数的底数),曲线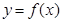 在点
在点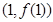 处的切线与x轴平行.
处的切线与x轴平行.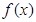 的单调区间;
的单调区间; 其中
其中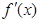 为
为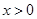 ,
,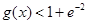 .
.
 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数). 在区间(0,+
在区间(0,+ )上为增函数,求整数m的最大值.
)上为增函数,求整数m的最大值. 为实数,
为实数,
 ;
; ,求
,求 在[-2,2] 上的最大值和最小值.
在[-2,2] 上的最大值和最小值.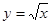 与直线x=a,y=0所围成封闭图形的面积为a,则a=____
与直线x=a,y=0所围成封闭图形的面积为a,则a=____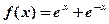 ,若曲线
,若曲线 上在点
上在点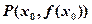 处的切线斜率为
处的切线斜率为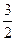
 ,则
,则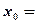 .
.