题目内容
 为实数,
为实数,
(1)求导数 ;
;
(2)若 ,求
,求 在[-2,2] 上的最大值和最小值.
在[-2,2] 上的最大值和最小值.
⑴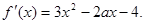 (2) 最大值为
(2) 最大值为 最小值为
最小值为
解析试题分析:⑴将括号打开函数变成多项式函数来求导数;也可利用积的导数法则来求解;(2)由 结合(1)的结果可求出a值,从而获得
结合(1)的结果可求出a值,从而获得 的具体解析式,进而获得导数
的具体解析式,进而获得导数 ,令其等于零,求得其可能极值,并求出端点的函数值,比较其大小就可求出
,令其等于零,求得其可能极值,并求出端点的函数值,比较其大小就可求出 在[-2,2] 上的最大值和最小值.
在[-2,2] 上的最大值和最小值.
试题解析:⑴由原式得 ∴
∴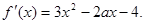
⑵由 得
得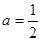 ,
,
此时有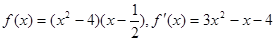 .
.
由 得
得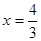 或x="-1" ,
或x="-1" ,
又
所以f(x)在[-2,2]上的最大值为 最小值为
最小值为
考点:1.函数求导;2.函数的最值.

练习册系列答案
相关题目
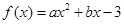 在
在 处取得极值,且在
处取得极值,且在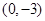 点处的切线与直线
点处的切线与直线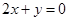 平行.
平行.  的解析式;
的解析式;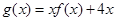 的单调递增区间及极值。
的单调递增区间及极值。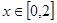 的最值。
的最值。 与
与 轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在
轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在 元
元 ,其它的三个边角地块每单位面积价值
,其它的三个边角地块每单位面积价值 元.
元.
 是
是 函数的两个极值点.
函数的两个极值点. 和
和 的值;
的值; 的极大值点还是极小值点,并求出相应极值.
的极大值点还是极小值点,并求出相应极值.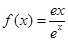 ,
, 。
。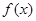 在
在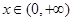 上的值域;
上的值域; ,对
,对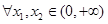 ,
,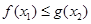 恒成立,
恒成立,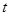 的取值范围
的取值范围 ,(
,(  为常数,
为常数, 为自然对数的底).
为自然对数的底). 时,求
时,求 ;
; 在
在 时取得极小值,试确定
时取得极小值,试确定 ,将
,将 ,试判断曲线
,试判断曲线 是否能与直线
是否能与直线 (
( 为确定的常数)相切,并说明理由.
为确定的常数)相切,并说明理由. 的极值
的极值 .
. 的方程f(x)=a在区间
的方程f(x)=a在区间 上有三个根,求a的取值范围.
上有三个根,求a的取值范围.
 的单调区间和极值;
的单调区间和极值; ,都存在
,都存在 ,使得
,使得 ,求
,求 的取值范围
的取值范围