题目内容
如图所示,在底面为直角梯形的四棱锥P ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=
ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=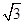 ,BC=4.
,BC=4.

(1)求证:BD⊥PC;
(2)求直线AB与平面PDC所成的角;
(3)设点E在棱PC上,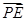 =λ
=λ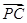 ,若DE∥平面PAB,求λ的值.
,若DE∥平面PAB,求λ的值.
 ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=
ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=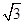 ,BC=4.
,BC=4.
(1)求证:BD⊥PC;
(2)求直线AB与平面PDC所成的角;
(3)设点E在棱PC上,
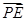 =λ
=λ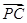 ,若DE∥平面PAB,求λ的值.
,若DE∥平面PAB,求λ的值.(1)见解析 (2)60° (3)

(1)证明:由题意知,AB⊥AD,AD=1,AB=
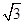 ,
,∴BD=2,BC=4,
∴DC=2
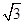 ,
,则BC2=DB2+DC2,
∴BD⊥DC,
∵PD⊥平面ABCD,
∴BD⊥PD,
而PD∩CD=D,
∴BD⊥平面PDC.
∵PC在平面PDC内,
∴BD⊥PC.
解:(2)如图所示,过D作DF∥AB交BC于F,过点F作FG⊥CD交CD于G.
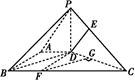
∵PD⊥平面ABCD,
∴平面PDC⊥平面ABCD,
∴FG⊥平面PDC,
∴∠FDG为直线AB与平面PDC所成的角.
在Rt△DFC中,∠DFC=90°,DF=
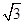 ,CF=3,
,CF=3,∴tan∠FDG=
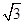 ,
,∴∠FDG=60°.
∴直线AB与平面PDC所成角为60°.
(3)连接EF,

∵DF∥AB,
∴DF∥平面PAB.
∵DE∥平面PAB,
∴平面DEF∥平面PAB,
∴EF∥AB,如图所示,
∵AD=1,BC=4,BF=1,
∴
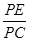 =
=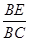 =
= ,
,∴
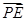 =
= ,
,即λ=
 .
.
练习册系列答案
相关题目

 关于直线
关于直线 对称,
对称,
 .把
.把 沿
沿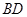 折起(如图二),使二面角
折起(如图二),使二面角 的余弦值等于
的余弦值等于 .对于图二,完成以下各小题:
.对于图二,完成以下各小题:
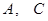 两点间的距离;
两点间的距离; 平面
平面 ;
; 所成角的正弦值.
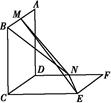
所成角的正弦值.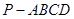 中,
中,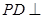 平面
平面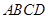 ,底面
,底面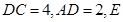 为
为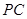 的中点.
的中点.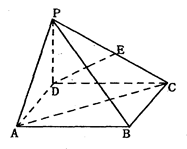
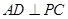 ;
;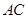 上是否存在一点
上是否存在一点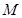 ,使得
,使得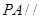 平面
平面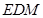 ?若存在,求出
?若存在,求出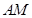 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.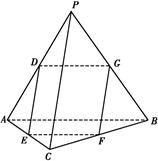
 是直线,
是直线, 、
、 是两个不同的平面,则( )
是两个不同的平面,则( ) ,
,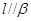 ,则
,则
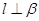 ,则
,则
 ,则
,则 β⊥γ”是真命题,如果把α、β、γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题的个数是________.
β⊥γ”是真命题,如果把α、β、γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题的个数是________.