题目内容
已知:平面α∩平面β=l,α⊥平面γ,β⊥平面γ.
求证:l⊥γ.

求证:l⊥γ.

见解析
证明:设α∩γ=m,β∩γ=n,
因为平面α∩平面β=l,
所以在l任意取一点P,过P在平面α内作PA⊥m,
因为α⊥平面γ,α∩γ=m,
所以PA⊥γ,
过P在平面β内作PB⊥n,
因为β⊥平面γ,β∩γ=n,
所以PB⊥γ,
所以PA,PB重合即为l,
所以l⊥γ.
因为平面α∩平面β=l,
所以在l任意取一点P,过P在平面α内作PA⊥m,
因为α⊥平面γ,α∩γ=m,
所以PA⊥γ,
过P在平面β内作PB⊥n,
因为β⊥平面γ,β∩γ=n,
所以PB⊥γ,
所以PA,PB重合即为l,
所以l⊥γ.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 ,
, ,
, ,N是BC的中点.如图所示,将梯形ABCD绕AB逆时针旋转
,N是BC的中点.如图所示,将梯形ABCD绕AB逆时针旋转 ,得到梯形
,得到梯形 .
.
 平面
平面 ;
;  平面
平面 ;
; 为正方形,四边形
为正方形,四边形 为等腰梯形,
为等腰梯形, ∥
∥ ,
, ,
, ,
, .
. 平面
平面 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.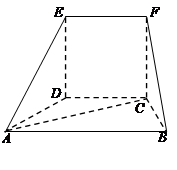
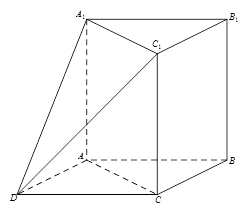
 中,
中, 平面
平面 ,
, .以
.以 ,
, 为邻边作平行
为邻边作平行 ,连接
,连接 和
和 .
. 
 平面
平面 ;
; 平面
平面 .
.
 ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=
ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=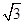 ,BC=4.
,BC=4.
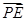 =λ
=λ ,若DE∥平面PAB,求λ的值.
,若DE∥平面PAB,求λ的值.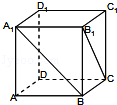
 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题:
是一条直线,以下命题: ,则
,则 ;②若
;②若 ,
, ,
,

 的侧棱
的侧棱 在下底面的射影
在下底面的射影 与
与 平行,若
平行,若 ,且
,且 ,则
,则 的余弦值为( )
的余弦值为( )



