Question

【题目】已知直线的参数方程为（t为参数，α∈[0，π）．以O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ＝ρcosθ+2，

（1）若，求直线的极坐标方程

（2）若直线与曲线C有唯一公共点，求α

Answer 1

【答案】（1）．（2）α＝0、或

【解析】

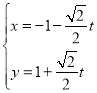（1）当时，直线l的参数方程为（t为参数），先转化为直角坐标方程，再得到直线l的极坐标方程.

（2）先将曲线C的极坐标方程ρ＝ρcosθ+2，化为直角坐标方程y2＝4x+4，再将参数方程代入y2＝4x+4，化简得t2sin2α+2t（sinα﹣2cosα）+1＝0，然后根据直线l曲线C一公共点，转化为关于t的方程t2sin2α+2t（sinα﹣2cosα）+1＝0，α∈[0，π）有唯一解求解.

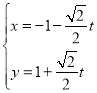（1）当时，直线l的参数方程为（t为参数），所以直角坐标方程为x+y＝0，

由于直线经过极点且倾斜角为，所以直线l的极坐标方程．

（2）ρ＝ρcosθ+2，所以ρ2＝（ρcosθ+2）2，

即x2+y2＝（x+2）2，即y2＝4x+4，

将参数方程代入y2＝4x+4，

化简得，t2sin2α+2t（sinα﹣2cosα）+1＝0

因为直线l曲线C一个公共点，

所以关于t的方程t2sin2α+2t（sinα﹣2cosα）+1＝0，α∈[0，π）有唯一解

①当sin2α＝0即α＝0时，符合题意；

②当cosα≠0时，[2（sinα﹣2cosα）]2﹣4sin2α＝0，

即cosα（cosα﹣sinα）＝0，

所以cosα＝0或cosα＝sinα，

又α∈[0，π），所以或

综上，直线l与曲线C唯一公共点时，α＝0、或