题目内容
【题目】为了迎接青奥会，南京将在主干道统一安装某种新型节能路灯，该路灯由灯柱和支架组成．在如图所示的直角坐标系中，支架ACB是抛物线y2=2x的一部分，灯柱CD经过该抛物线的焦点F且与路面垂直，其中C在抛物线上，B为抛物线的顶点，DH表示道路路面，BF∥DH，A为锥形灯罩的顶，灯罩轴线与抛物线在A处的切线垂直．安装时要求锥形灯罩的顶到灯柱的距离是1.5米，灯罩的轴线正好通过道路路面的中线．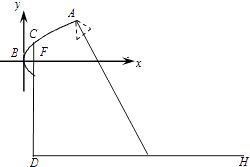 
（1）求灯罩轴线所在的直线方程；
（2）若路宽为10米，求灯柱的高．
【答案】
（1）解：由题意知，BF= 
，则xA=1.5+ =2，
代入y2=2x得yA=2，故A（2，2）．
设点A处的切线方程为y﹣2=k（x﹣2），
代入抛物线方程y2=2x消去x，得ky2﹣2y+4﹣4k=0．
则△=4﹣4k（4﹣4k）=0，解得k= ．
故灯罩轴线的斜率为﹣2，其方程为y﹣2=﹣2（x﹣2），即y=﹣2x+6
（2）解：由于路宽为10，则当x= 
时，y=﹣5，从而FD=5．
又CF=1，则CD=6．
答：灯柱的高为6米
【解析】（1）求出A的坐标，设点A处的切线方程，代入抛物线方程，求出斜率，即可得出灯罩轴线所在的直线方程；（2）求出FD，利用CF，可求灯柱的高．
【考点精析】解答此题的关键在于理解基本不等式在最值问题中的应用的相关知识，掌握用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”．
练习册系列答案
相关题目
