题目内容
【题目】对于定义域为D的函数y=f(x),若同时满足下列条件:
①f(x)在D内单调递增或单调递减;
②存在区间[a,b]D,使f(x)在[a,b]上的值域为[a,b];那么把y=f(x)(x∈D)叫闭函数.
(1)求闭函数y=﹣x3符合条件②的区间[a,b]
(2)判断函数f(x)= ![]() 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若y=k+ ![]() 是闭函数,求实数k的范围.
是闭函数,求实数k的范围.
【答案】
(1)解:由题意,y=﹣x3在[a,b]上递减,则 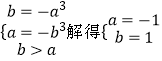 ,
,
所以,所求的区间为[﹣1,1]
(2)解: ![]() ,在(﹣∞,﹣1)上单调递增,在(﹣1,+∞)上单调递增,
,在(﹣∞,﹣1)上单调递增,在(﹣1,+∞)上单调递增,
所以,函数在定义域上不单调递增或单调递减,从而该函数不是闭函数
(3)解:若 ![]() 是闭函数,则存在区间[a,b],在区间[a,b]上,
是闭函数,则存在区间[a,b],在区间[a,b]上,
函数f(x)的值域为[a,b],即 ![]() ,
,
∴ ![]() 的两个实数根,
的两个实数根,
即方程x2﹣(2k+1)x+k2﹣2=0(x≥﹣2,x≥k)有两个不等的实根.
当 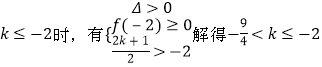 .
.
当 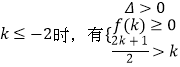 此不等式组无解.
此不等式组无解.
综上所述, ![]()
【解析】(1)根据函数的单调性得到关于a,b的方程组,解出即可;(2)将f(x)变形,得到f(x)的单调区间,根据闭函数的定义判断即可;(3)根据闭函数的定义得到方程x2﹣(2k+1)x+k2﹣2=0(x≥﹣2,x≥k)有两个不等的实根,通过讨论k,得到关于k的不等式组,解出即可.
【考点精析】关于本题考查的函数单调性的判断方法和函数单调性的性质,需要了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集才能得出正确答案.

练习册系列答案
相关题目