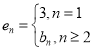题目内容
【题目】棋盘上标有第![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 站,棋子开始位于第
站,棋子开始位于第![]() 站,棋手抛掷均匀硬币走跳棋游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到调到第
站,棋手抛掷均匀硬币走跳棋游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到调到第![]() 站或第
站或第![]() 站时,游戏结束.设棋子位于第
站时,游戏结束.设棋子位于第![]() 站的概率为
站的概率为![]() .
.
(1)当游戏开始时,若抛掷均匀硬币![]() 次后,求棋手所走步数之和
次后,求棋手所走步数之和![]() 的分布列与数学期望;
的分布列与数学期望;
(2)证明:![]() ;
;
(3)求![]() 、
、![]() 的值.
的值.
【答案】(1)分布列见解析,随机变量![]() 的数学期望为
的数学期望为![]() ;(2)证明见解析;
;(2)证明见解析;
(3)![]() ,
,![]() .
.
【解析】
(1)根据题意得出随机变量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() 、
、![]() ,利用独立重复试验的概率公式计算出随机变量
,利用独立重复试验的概率公式计算出随机变量![]() 在相应取值时的概率,可列出随机变量
在相应取值时的概率,可列出随机变量![]() 的分布列,由此计算出随机变量
的分布列,由此计算出随机变量![]() 的数学期望;
的数学期望;
(2)根据题意,棋子要到第![]() 站,由两种情况,由第
站,由两种情况,由第![]() 站跳
站跳![]() 站得到,也可以由第
站得到,也可以由第![]() 站跳
站跳![]() 站得到,由此得出
站得到,由此得出![]() ,并在该等式两边同时减去
,并在该等式两边同时减去![]() ,可得出所证等式成立;
,可得出所证等式成立;
(3)结合(1)、(2)可得![]() ,利用累加法求出数列
,利用累加法求出数列![]() 的通项公式,从而可求出
的通项公式,从而可求出![]() 和
和![]() 的值.
的值.
(1)由题意可知,随机变量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() 、
、![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以,随机变量![]() 的分布列如下表所示:
的分布列如下表所示:
|
|
|
|
|
|
|
|
|
|
所以,随机变量![]() 的数学期望为
的数学期望为![]() ;
;
(2)根据题意,棋子要到第![]() 站,由两种情况,由第
站,由两种情况,由第![]() 站跳
站跳![]() 站得到,其概率为
站得到,其概率为![]() ,也可以由第
,也可以由第![]() 站跳
站跳![]() 站得到,其概率为
站得到,其概率为![]() ,所以,
,所以,![]() .
.
等式两边同时减去![]() 得
得![]() ;
;
(3)由(2)可得![]() ,
,![]() ,
,![]() .
.
由(2)可知,数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
![]() ,
,
![]()
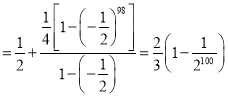 ,
,
又![]() ,则
,则![]() ,
,
由于若跳到第![]() 站时,自动停止游戏,故有
站时,自动停止游戏,故有![]() .
.

【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
【题目】我们知道,地球上的水资源有限,爱护地球、节约用水是我们每个人的义务与责任.某市政府为了对自来水的使用进行科学管理,节约水资源,计划确定一个家庭年用水量的标准.为此,对全市家庭日常用水量的情况进行抽样抽查,获得了![]() 个家庭某年的用水量(单位:立方米),统计结果如下表及图所示.
个家庭某年的用水量(单位:立方米),统计结果如下表及图所示.
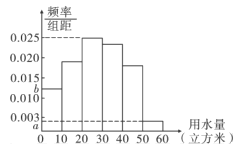
分组 | 频数 | 频率 |
| 25 | |
| 0.19 | |
| 50 | |
| 0.23 | |
| 0.18 | |
| 5 |
(1)分别求出![]() ,
,![]() 的值;
的值;
(2)若以各组区间中点值代表该组的取值,试估计全市家庭年均用水量;
(3)从样本中年用水量在![]() (单位:立方米)的5个家庭中任选3个,作进一步的跟踪研究,求年用水量最多的家庭被选中的概率(5个家庭的年用水量都不相等).
(单位:立方米)的5个家庭中任选3个,作进一步的跟踪研究,求年用水量最多的家庭被选中的概率(5个家庭的年用水量都不相等).