题目内容
已知点的序列An(xn,0),n∈N,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段An-2An-1的中点,….
(1)写出xn与xn-1、xn-2之间关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明;
(3)求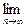 xn
xn
(1)写出xn与xn-1、xn-2之间关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明;
(3)求
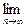 xn
xn(1) xn=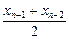 ; (2) an=(-
; (2) an=(-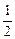 )n-1a(n∈N) ,(3)
)n-1a(n∈N) ,(3)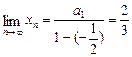 a
a
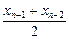 ; (2) an=(-
; (2) an=(-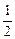 )n-1a(n∈N) ,(3)
)n-1a(n∈N) ,(3)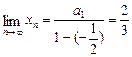 a
a (1)当n≥3时,xn=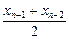 ;
;
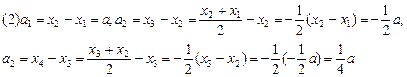
由此推测an=(-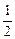 )n-1a(n∈N)
)n-1a(n∈N)
证法一:因为a1=a>0,且
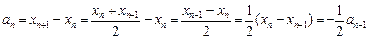 (n≥2)
(n≥2)
所以an=(-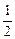 )n-1a
)n-1a
证法二: 用数学归纳法证明:
(ⅰ)当n=1时,a1=x2-x1=a=(-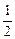 )0a,公式成立;
)0a,公式成立;
(ⅱ)假设当n=k时,公式成立,即ak=(-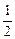 )k-1a成立.
)k-1a成立.
那么当n=k+1时,
ak+1=xk+2-xk+1=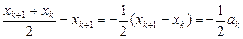
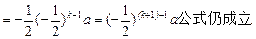
据(ⅰ)(ⅱ)可知,对任意n∈N,公式an=(-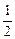 )n-1a成立.
)n-1a成立.
(3)当n≥3时,有
xn=(xn-xn-1)+(xn-1-xn-2)+…+(x2-x1)+x1=an-1+an-2+…+a1,
由(2)知{an}是公比为-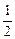 的等比数列,所以
的等比数列,所以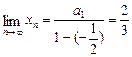 a.
a.
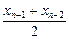 ;
;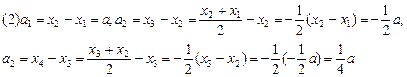
由此推测an=(-
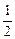 )n-1a(n∈N)
)n-1a(n∈N)证法一:因为a1=a>0,且
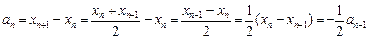 (n≥2)
(n≥2)所以an=(-
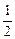 )n-1a
)n-1a
证法二: 用数学归纳法证明:
(ⅰ)当n=1时,a1=x2-x1=a=(-
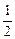 )0a,公式成立;
)0a,公式成立;(ⅱ)假设当n=k时,公式成立,即ak=(-
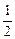 )k-1a成立.
)k-1a成立.那么当n=k+1时,
ak+1=xk+2-xk+1=
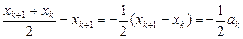
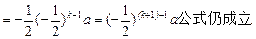
据(ⅰ)(ⅱ)可知,对任意n∈N,公式an=(-
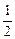 )n-1a成立.
)n-1a成立.(3)当n≥3时,有
xn=(xn-xn-1)+(xn-1-xn-2)+…+(x2-x1)+x1=an-1+an-2+…+a1,
由(2)知{an}是公比为-
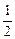 的等比数列,所以
的等比数列,所以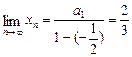 a.
a.
练习册系列答案
相关题目
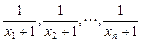 为等差数列.
为等差数列.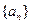 是由正数组成的比数列,
是由正数组成的比数列,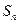 是其前
是其前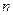 项和.
项和.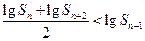 ;
;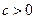 ,使得
,使得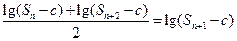 成立?并证明你的结论.
成立?并证明你的结论.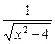 (x<-2).
(x<-2).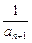 =-f--1(an)(n∈N*),求an;
=-f--1(an)(n∈N*),求an;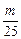 成立?若存在,求出m的值;若不存在,说明理由.
成立?若存在,求出m的值;若不存在,说明理由.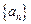 中,
中,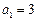 ,
,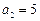 ,其前
,其前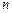 项和
项和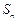 满足
满足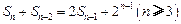 .令
.令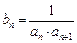 .
.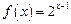 ,求证:
,求证: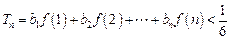 (
(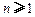 );
);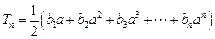 (
(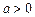 ),求同时满足下列两个条件的所有
),求同时满足下列两个条件的所有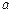 的值:①对于任意正整数
的值:①对于任意正整数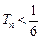 ;②对于任意的
;②对于任意的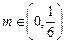 ,均存在
,均存在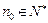 ,使得
,使得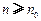 时,
时,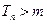 .
.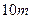 ,在第一面小旗处有某人把小旗全部集中到一面小旗的位置上,每次只能拿一面小旗,要使他走的路最短,应集中到哪一面小旗的位置上?最短路程是多少?
,在第一面小旗处有某人把小旗全部集中到一面小旗的位置上,每次只能拿一面小旗,要使他走的路最短,应集中到哪一面小旗的位置上?最短路程是多少?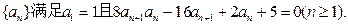 求数列
求数列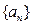 的通项公式.
的通项公式. 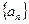 中,
中,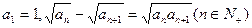 ,则
,则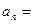 .
.