题目内容
【题目】如图,在正△ABC中,点D,E分别在边AC, AB上,且AD=![]() AC,AE=
AC,AE=![]() AB,BD,CE相交于点F.
AB,BD,CE相交于点F.
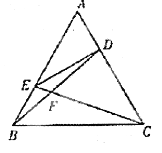
(Ⅰ)求证:A,E,F,D四点共圆;
(Ⅱ)若正△ABC的边长为2,求A,E,F,D所在圆的半径.
【答案】(1)证明过程详见解析;(2)![]() .
.
【解析】试题本题以正三角形为几何背景,考查四点共圆问题以及相似三角形问题,考查学生的转化与化归的能力.第一问,利用已知条件中边的比例关系可得出结论![]() ,再利用三角形相似,得出
,再利用三角形相似,得出![]() ,所以
,所以![]() ,所以可证
,所以可证![]() 四点共圆;第二问,根据所给正三角形的边长为2,利用已知的比例关系,得出各个小边的长度,从而得出
四点共圆;第二问,根据所给正三角形的边长为2,利用已知的比例关系,得出各个小边的长度,从而得出![]() 为正三角形,所以得出
为正三角形,所以得出![]() ,所以
,所以![]() 是
是![]() 所在圆的圆心,而
所在圆的圆心,而![]() 是半径,即为
是半径,即为![]() .
.
试题解析:(Ⅰ)证明:∵![]() , ∴
, ∴![]() ,
,
∵在正![]() 中,
中,![]() , ∴
, ∴![]() ,
,
又∵![]() ,
,![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
即![]() ,所以
,所以![]() 四点共圆. 5分
四点共圆. 5分
(Ⅱ)解:如图,
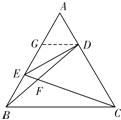
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
∵![]() ,
,![]() , ∴
, ∴![]() 为正三角形,
为正三角形,
∴![]() ,即
,即![]() ,
,
所以点![]() 是
是![]() 外接圆的圆心,且圆
外接圆的圆心,且圆![]() 的半径为
的半径为![]() .
.
由于![]() 四点共圆,即
四点共圆,即![]() 四点共圆
四点共圆![]() ,其半径为
,其半径为![]() . 10分
. 10分

练习册系列答案
相关题目
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: ,
,![]() .
.