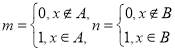题目内容
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 分别是
分别是![]() 的中点,点
的中点,点![]() 在棱
在棱![]()
上, ![]() (
(![]() ).
).

(Ⅰ)三棱锥![]() 的体积分别为
的体积分别为![]() ,当
,当![]() 为何值时,
为何值时, ![]() 最大?最大值为多少?
最大?最大值为多少?
(Ⅱ)若![]() 平面
平面![]() ,证明:平面
,证明:平面![]() 平面
平面![]() .
.
【答案】(Ⅰ)![]() ,
,![]() .(Ⅱ)见解析.
.(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)由题可知, ![]() ,由
,由![]() 和
和![]() ,结合基本不等式可求最值;
,结合基本不等式可求最值;
(Ⅱ)连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() 为
为![]() 的中点,可得
的中点,可得![]() 为
为![]() 中点,易证得
中点,易证得![]() ,
, ![]() 得
得![]() 平面
平面![]() ,所以
,所以![]() ,进而可证得
,进而可证得![]() ,
, ![]() ,所以
,所以![]() 平面因为
平面因为![]() 平面
平面![]() ,从而得证.
,从而得证.
试题解析:
(Ⅰ)由题可知, ![]() ,
,
![]()
![]() .
.
所以![]() (当且仅当
(当且仅当![]() ,即
,即![]() 时等号成立)
时等号成立)
所以当![]() 时,
时, ![]() 最大,最大值为
最大,最大值为![]() .
.
(Ⅱ)连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() 为
为![]() 的中点,因为
的中点,因为![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() 为
为![]() 中点.连接
中点.连接![]() ,
,
因为![]() 为中点,所以
为中点,所以![]() ,因为
,因为![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,因为
,因为![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() .同理
.同理![]() ,因为
,因为![]() ,所以
,所以![]() 平面因为
平面因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面.
平面.

练习册系列答案
相关题目