题目内容
已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当x>0时,f(x)=lnx-ax,若函数在定义域上有且仅有4个零点,则实数a的取值范围是( )
| A.(e,+∞) | B.(0, ) ) |
C.(1, ) ) | D.(-∞, ) ) |
B
由于函数f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,所以其图象关于y轴对称,所以只要考虑当x>0时,f(x)=lnx-ax有且仅有2个不同的零点即可,由于f′(x)=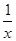 -a,当f′(x)=
-a,当f′(x)=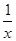 -a=0时,x=
-a=0时,x=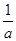 (x>0),所以a>0,当x∈(0,
(x>0),所以a>0,当x∈(0,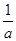 )时,f′(x)>0,函数f(x)单调递增,当x∈(
)时,f′(x)>0,函数f(x)单调递增,当x∈(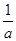 ,+∞)时,f′(x)<0,函数f(x)单调递减,所以当x=
,+∞)时,f′(x)<0,函数f(x)单调递减,所以当x=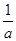 时,f(x)max=f()=ln
时,f(x)max=f()=ln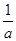 -1,要使x>0时,f(x)=lnx-ax有且仅有2个不同的零点,只需f(
-1,要使x>0时,f(x)=lnx-ax有且仅有2个不同的零点,只需f(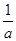 )=ln
)=ln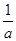 -1>0,解得0<a<
-1>0,解得0<a< .故选B.
.故选B.
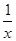 -a,当f′(x)=
-a,当f′(x)=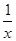 -a=0时,x=
-a=0时,x=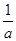 (x>0),所以a>0,当x∈(0,
(x>0),所以a>0,当x∈(0,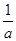 )时,f′(x)>0,函数f(x)单调递增,当x∈(
)时,f′(x)>0,函数f(x)单调递增,当x∈(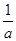 ,+∞)时,f′(x)<0,函数f(x)单调递减,所以当x=
,+∞)时,f′(x)<0,函数f(x)单调递减,所以当x=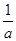 时,f(x)max=f()=ln
时,f(x)max=f()=ln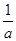 -1,要使x>0时,f(x)=lnx-ax有且仅有2个不同的零点,只需f(
-1,要使x>0时,f(x)=lnx-ax有且仅有2个不同的零点,只需f(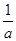 )=ln
)=ln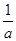 -1>0,解得0<a<
-1>0,解得0<a< .故选B.
.故选B.
练习册系列答案
相关题目
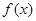 ,当
,当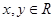 时,恒有
时,恒有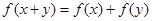 .
.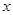 为正实数,
为正实数,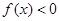 ,并且
,并且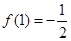 ,试求
,试求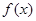 是定义在R上的奇函数且单调递增,当
是定义在R上的奇函数且单调递增,当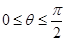 时,
时,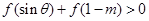 恒成立,则实数
恒成立,则实数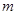 的取值范围是( )
的取值范围是( )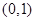
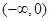
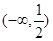
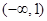
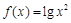 的单调递减区间是________.
的单调递减区间是________.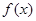 是定义在区间
是定义在区间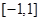 上的奇函数,且
上的奇函数,且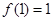 ,若
,若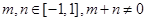 时,有
时,有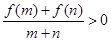 .
.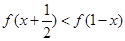 ;
;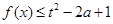 对
对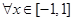 与
与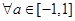 恒成立,求实数
恒成立,求实数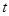 的取值范围.
的取值范围.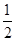 ,1]上恒成立,求实数a的取值范围.
,1]上恒成立,求实数a的取值范围.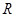 上的函数
上的函数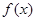 满足
满足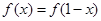 ,且当
,且当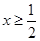 时,
时,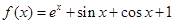 ,则有( )
,则有( )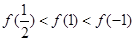
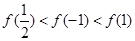
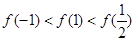
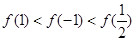
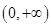 的单调函数
的单调函数 ,对任意的
,对任意的 ,都有
,都有 ,若
,若 是方程
是方程 的一个解,则
的一个解,则