题目内容
已知函数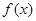 ,当
,当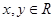 时,恒有
时,恒有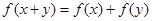 .
.
(1)求证: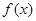 是奇函数;
是奇函数;
(2)如果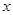 为正实数,
为正实数,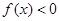 ,并且
,并且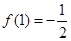 ,试求
,试求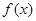 在区间[-2,6]上的最值.
在区间[-2,6]上的最值.
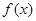 ,当
,当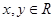 时,恒有
时,恒有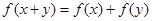 .
.(1)求证:
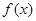 是奇函数;
是奇函数;(2)如果
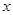 为正实数,
为正实数,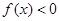 ,并且
,并且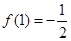 ,试求
,试求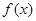 在区间[-2,6]上的最值.
在区间[-2,6]上的最值.(1)证明见解析;(2)最大值为1,最小值为-3..
试题分析:解题思路:(1)利用奇函数的定义进行证明;(2)先证明
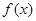 的单调性,再求在
的单调性,再求在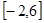 的最值.
的最值.规律总结:(1)证明函数奇偶性的步骤:①验证函数定义域是否关于原点对称,②判断
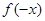 与
与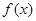 的关系,③下结论;(2)先利用函数单调性的定义证明函数的单调性,再根据单调性求最值.注意点:判定或证明函数的奇偶性时,一定不要忘记验证函数的定义域是否关于原点对称.
的关系,③下结论;(2)先利用函数单调性的定义证明函数的单调性,再根据单调性求最值.注意点:判定或证明函数的奇偶性时,一定不要忘记验证函数的定义域是否关于原点对称.试题解析: (1)函数定义域为
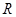 ,其定义域关于原点对称,
,其定义域关于原点对称,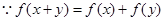 ,令
,令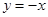 ,
,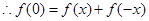 ,令
,令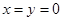 ,
,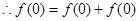 ,得
,得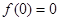 .
. ,得
,得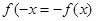 ,
,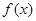 为奇函数.
为奇函数.(2)设
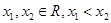 .
.则
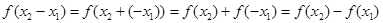 .
.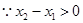 ,
,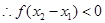 ,
,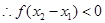 ,即
,即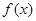 在
在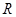 上单调递减.
上单调递减.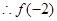 为最大值,
为最大值, 为最小值.
为最小值.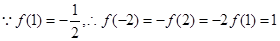 ,
,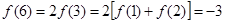 .
.∴
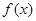 在区间
在区间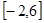 上的最大值为1,最小值为-3.
上的最大值为1,最小值为-3.
练习册系列答案
相关题目
 上的三个函数
上的三个函数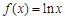 ,
, ,
, ,且
,且 在
在 处取得极值.
处取得极值.

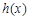 的单调区间.
的单调区间.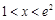 时,恒有
时,恒有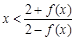 成立.
成立.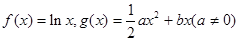 .
.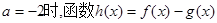 在其定义域内是增函数,求b的取值范围;
在其定义域内是增函数,求b的取值范围;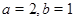 ,若函数
,若函数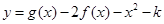 在 [1,3]上恰有两个不同零点,求实数
在 [1,3]上恰有两个不同零点,求实数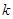 的取值范围.
的取值范围.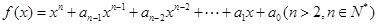 ,设
,设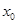 是函数
是函数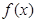 的零点的最大值,则下列论断一定错误的是( )
的零点的最大值,则下列论断一定错误的是( )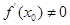
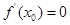
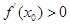
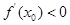
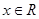 ,关于
,关于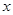 的函数
的函数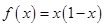 ,则下列结论中正确的是( )
,则下列结论中正确的是( )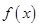 有最大值
有最大值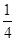
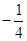
 )
)