题目内容
设定义域为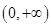 的单调函数
的单调函数 ,对任意的
,对任意的 ,都有
,都有 ,若
,若 是方程
是方程 的一个解,则
的一个解,则 可能存在的区间是( )
可能存在的区间是( )
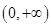 的单调函数
的单调函数 ,对任意的
,对任意的 ,都有
,都有 ,若
,若 是方程
是方程 的一个解,则
的一个解,则 可能存在的区间是( )
可能存在的区间是( )A. | B.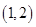 | C. | D. |
B
试题分析:由于函数
 在其定义域
在其定义域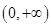 上单调,则存在唯一实数
上单调,则存在唯一实数 使得
使得 ,对任意的
,对任意的 ,都有
,都有 ,则
,则 ,由于
,由于 ,
,因此
 ,因为函数
,因为函数 在区间
在区间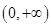 上单调递增,且
上单调递增,且 ,所以
,所以 ,故
,故 ,令
,令 ,则
,则 在区间
在区间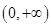 上单调递增,且
上单调递增,且 ,
, ,故
,故 ,故选B.
,故选B.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
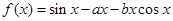
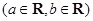 .
.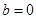 ,讨论函数
,讨论函数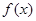 在区间
在区间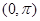 上的单调性;
上的单调性;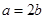 且
且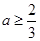 ,对任意的
,对任意的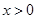 ,试比较
,试比较 的大小.
的大小. )
)
 .
. 的奇偶性;
的奇偶性; 上为减函数,求
上为减函数,求 的取值范围.
的取值范围.


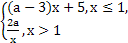 是(-∞,+∞)上的减函数,则a的取值范围是
是(-∞,+∞)上的减函数,则a的取值范围是



 ,g(x)=x2f(x-1),则函数g(x)的递减区间是________.
,g(x)=x2f(x-1),则函数g(x)的递减区间是________.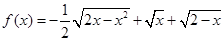 的最大值为 .
的最大值为 .