题目内容
已知f(x)是偶函数，且f(x)在[0，＋∞)上是增函数，如果f(ax＋1)≤f(x－2)在x∈[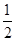
，1]上恒成立，求实数a的取值范围．
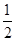，1]上恒成立，求实数a的取值范围．[－2,0]
解：由于f(x)为偶函数，且在[0，＋∞)上为增函数，由f(ax＋1)≤f(x－2)，则|ax＋1|≤|x－2|.又x∈[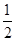，1]，故|x－2|＝2－x，即x－2≤ax＋1≤2－x.
∴1－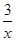
≤a≤
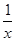－1在[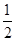，1]上恒成立．
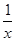(－1)min＝0，(1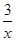－)max＝－2，
∴－2≤a≤0.
故a的取值范围为[－2,0]．
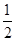，1]，故|x－2|＝2－x，即x－2≤ax＋1≤2－x.∴1－
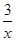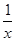≤a≤－1在[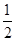，1]上恒成立．(
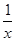－1)min＝0，(1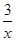－)max＝－2，∴－2≤a≤0.
故a的取值范围为[－2,0]．
练习册系列答案
相关题目
．
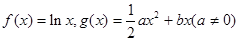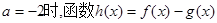在其定义域内是增函数，求b的取值范围；
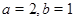，若函数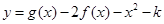
在 [1，3]上恰有两个不同零点，求实数
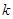的取值范围．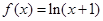
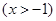
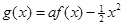
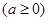的单调性。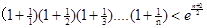
)
)
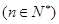
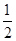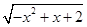的单调递增区间是( )
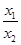)＝f(x1)－f(x2)，且当x>1时，f(x)<0.
＋
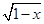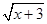的最大值为M，最小值为m，则
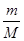的值为( )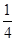
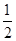
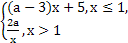是(-∞,+∞)上的减函数,则a的取值范围是
，g(x)＝x2f(x－1)，则函数g(x)的递减区间是________．