题目内容
【题目】在直角坐标系xOy中,圆C的参数方程![]() (
(![]() 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线 l 的极坐标方程是 ![]() ,射线OM:
,射线OM:![]() 与圆C的交点为O、P,与直线 l 的交点为Q,求线段PQ的长.
与圆C的交点为O、P,与直线 l 的交点为Q,求线段PQ的长.
【答案】
(1)
解:圆 ![]() 的普通方程为
的普通方程为 ![]() ,又
,又 ![]() ,所以圆
,所以圆 ![]() 的极坐标方程为
的极坐标方程为 ![]() ;
;
(2)
解:设 ![]() 为点
为点 ![]() 的极坐标,则有
的极坐标,则有 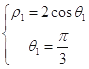 ,解得
,解得 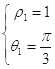 ,设
,设 ![]() 为点
为点 ![]() 的极坐标,
的极坐标, 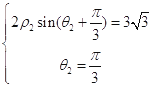 ,解得
,解得 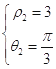 ,由于
,由于 ![]() ,所以
,所以 ![]() ,所以线段
,所以线段 ![]() 的长为2.
的长为2.
【解析】本题主要考查了圆的极坐标方程,解决问题的关键是(1)由圆C的参数方程 ![]() 为参数),化为普通方程为
为参数),化为普通方程为 ![]() ,利用
,利用 ![]() ,即得圆C的极坐标方程;(2)求线段
,即得圆C的极坐标方程;(2)求线段 ![]() 的长,由于
的长,由于 ![]() 三点共线,故
三点共线,故 ![]() ,可设
,可设 ![]()
![]() ,
, ![]()
![]() ,则
,则 ![]() ,关键是求出
,关键是求出 ![]() 的值,由
的值,由 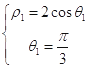 可求得
可求得 ![]() 的值,由
的值,由 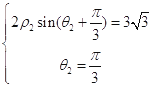 可求得
可求得 ![]() 的值,从而可解.
的值,从而可解.
【考点精析】关于本题考查的圆的参数方程,需要了解圆![]() 的参数方程可表示为
的参数方程可表示为![]() 才能得出正确答案.
才能得出正确答案.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】兰州一中在世界读书日期间开展了“书香校园”系列读书教育活动。为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,且将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”。
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 |

(1)根据已知条件完成下面2×2列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
(2)利用分层抽样从这100名学生的“读书迷”中抽取8名进行集训,从中选派2名参加兰州市读书知识比赛,求至少有一名男生参加比赛的概率。
附: 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |


