题目内容
【题目】某校高一举行了一次数学竞赛，为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在[50，60），[90，100]的数据）．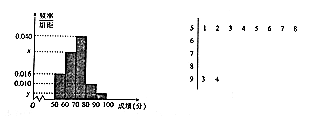 
（1）求样本容量n和频率分布直方图中的x，y的值；
（2）估计本次竞赛学生成绩的中位数和平均分；
（3）在选取的样本中，从竞赛成绩在80分以上（含80分）的学生中随机抽取2名学生，求所抽取的2名学生中至少有一人得分在[90，100]内的频率．
【答案】
（1）解：由题意可知，样本容量n= 
=50，y= 
=0.004，x=0.100﹣0.004﹣0.010﹣0.016﹣0.040=0.030
（2）解：设本次竞赛学生成绩的中位数为m，平均分为 
，
则[0.016+0.03+（m﹣70）×0.040]×10=0.5，解得m=71，
=（55×0.016+65×0.030+75×0.040+85×0.010+95×0.004]×10=70.6
（3）解：由题意可知，分数在[80，90）内的学生有5人，记这5人分别为a1，a2，a3，a4，a5，
分数在[90，100]内的学生有2人，记这2人分别为b1，b2．抽取的2名学生的所有情况有21种，
分别为：（a1，a2），（a1，a3），（a1，a4），（a1，a5），（a1，b1），（a1，b2），（a2，a3），
（a2，a4），（a2，a5），（a2，b1），（a2，b2），（a3，a4），（a3，a5），（a3，b1），
（a3，b2），（a4，a5），（a4，b1），（a4，b2），（a5，b1），（a5，b2），（b1，b2）．
其中2名同学的分数都不在[90，100]内的情况有10种，分别为：
（a1，a2），（a1，a3），（a1，a4），（a1，a5），（a2，a3），（a2，a4），（a2，a5），
（a3，a4），（a3，a5），（a4，a5）．
∴所抽取的2名学生中至少有一人得分在[90，100]内的概率P=1﹣ 
= 
【解析】（1）由样本容量和频数频率的关系易得答案；（2）根据平均数的定义和中位数的定义即可求出．（3）由题意可知，分数在[80，90）内的学生有5人，记这5人分别为a1 ， a2 ， a3 ， a4 ， a5 ， 分数在[90，100]内的学生有2人，记这2人分别为b1 ， b2 ， 列举法易得
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识，掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息，以及对平均数、中位数、众数的理解，了解⑴平均数、众数和中位数都是描述一组数据集中趋势的量；⑵平均数、众数和中位数都有单位；⑶平均数反映一组数据的平均水平，与这组数据中的每个数都有关系，所以最为重要，应用最广；⑷中位数不受个别偏大或偏小数据的影响；⑸众数与各组数据出现的频数有关，不受个别数据的影响，有时是我们最为关心的数据．
