题目内容

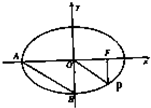
如图，从椭圆
x2
a2
+
y2
b2
=1（a＞b＞o）上一点P向x轴作垂线，垂足恰好为左焦点F1，又点A是椭圆与x轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，则椭圆的离心率e=______．
设F1（-c，0），将x=-c代入
x2
a2
+
y2
b2
=1（a＞b＞0），得y=±
b2
a

∴PF1=
b2
a
，OF1=c
∵AB∥OP，∴tan∠POF1=tan∠BAO=
b
a

∴在直角三角形POF1中，tan∠POF1=
PF1
OF1
=
b2
ac
=
b
a

∴b=c，∴a=
2
c
∴e=
c
a
=
2
2
．
故答案为：
2
2
．
练习册系列答案
相关题目
在焦点在x轴的椭圆过点P（3，0），且长轴长是短轴长的3倍，则其标准方程为______．
已知P点在以坐标轴为对称轴的椭圆上，点P到两焦点的距离分别为
4
5
3
和
2
5
3
，过P作长轴的垂线恰好过椭圆的右焦点，求椭圆方程．
已知点P为椭圆C：
x2
4
+
y2
3
=1上动点，F1，F2分别是椭圆C的焦点，则|PF1|-|PF2|的最大值为（　　）
A．2B．3C．2
3
D．4
点P在椭圆
x2
25
+
y2
9
=1上，F1，F2为两个焦点，若△F1PF2为直角三角形，这样的点P共有（　　）
A．4个B．5个C．6个D．8个
如图，函数y=f（x）的图象是中心在原点、焦点在x轴上的椭圆的两段弧，则不等式f（x）＜f（-x）+x的解集为（　　）
A．{x|-
2
＜x＜0或
2
＜x≤2}		B．{x|-2≤x＜-
2
或
2
＜x≤2}
C．{x|-2≤x＜-
2
2
或
2
2
＜x≤2}		D．{x|-
2
＜x＜
2
，且x≠0}
已知集合A={x|-2≤x≤10，x∈Z}，m，n∈A，方程
x2
m
+
y2
n
=1表示焦点在x轴上的椭圆，则这样的椭圆共有______个．
如图，椭圆的标准方程为
x2
a2
+
y2
b2
=1(a＞b＞0)，P为椭圆上的一点，且满足PF1⊥PF2，
（1）求三角形PF1F2的面积．
（2）若此椭圆长轴为8，离心率为
3
2
，求点P的坐标．
如图点F是椭圆的焦点，P是椭圆上一点，A，B是椭圆的顶点，且PF⊥x轴，OP∥AB，那么该椭圆的离心率是（　　）
A．
2
4
B．
1
2
C．
2
2
D．
3
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网