题目内容
16.已知$\overrightarrow{a}$•$\overrightarrow{c}$-$\overrightarrow{b}$•$\overrightarrow{c}$=-|$\overrightarrow{a}$-$\overrightarrow{b}$|•|$\overrightarrow{c}$|≠0,且$\overrightarrow{a}$和$\overrightarrow{b}$不垂直,则$\overrightarrow{a}$-$\overrightarrow{b}$与($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$( )| A. | 相等 | B. | 方向相同 | C. | 方向相反 | D. | 方向相同或相反 |
分析 变形得出∴($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{c}$=-|$\overrightarrow{a}$-$\overrightarrow{b}$|•|$\overrightarrow{c}$|≠0,即$\overrightarrow{a}$$-\overrightarrow{b}$与$\overrightarrow{c}$方向相反,
利用$\overrightarrow{a}$$•\overrightarrow{b}$为实数,且不为零,($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$与$\overrightarrow{c}$是共线向量,方向不确定,可选择答案.
解答 解:∵$\overrightarrow{a}$•$\overrightarrow{c}$-$\overrightarrow{b}$•$\overrightarrow{c}$=-|$\overrightarrow{a}$-$\overrightarrow{b}$|•|$\overrightarrow{c}$|≠0,
∴($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{c}$=-|$\overrightarrow{a}$-$\overrightarrow{b}$|•|$\overrightarrow{c}$|≠0,
即$\overrightarrow{a}$$-\overrightarrow{b}$与$\overrightarrow{c}$方向相反,
∵$\overrightarrow{a}$和$\overrightarrow{b}$不垂直,
∴∴$\overrightarrow{a}$-$\overrightarrow{b}$与($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$是共线向量,
故选:D.
点评 本题考察了平面向量的数量积,共线向量的概念,几何意义,属于容易题.

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. | 6+△x | B. | 6+△x+$\frac{9}{△x}$ | C. | 3+△x | D. | 9+△x |
| A. | -1 | B. | $-\frac{2}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
| A. | [0,1)∪(1,+∞) | B. | (-∞,1) | C. | (-∞,1)∪(1,+∞) | D. | (1,+∞) |
| A. | c<b<a | B. | a<b<c | C. | b<a<c | D. | a<c<b |
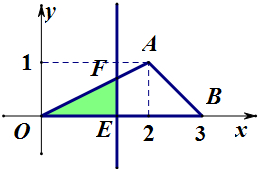 如图,在△AOB中,点A(2,1),B(3,0),点E在射线OB上自O开始向右移动.设OE=x,过E作OB的垂线l,记△AOB在直线l左边部分的面积为S,试写出S与x的函数关系式,并画出大致的图象.
如图,在△AOB中,点A(2,1),B(3,0),点E在射线OB上自O开始向右移动.设OE=x,过E作OB的垂线l,记△AOB在直线l左边部分的面积为S,试写出S与x的函数关系式,并画出大致的图象.