题目内容
已知向量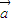
=（x，-1），
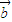=（3，y），其中x随机选自集合{-1，1，3}，y随机选自集合{1，3}，那么
⊥
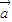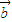的概率是 ．
【答案】分析：由于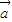
⊥
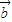等价于 
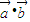=0，即3x-y=0，即 y=3x，所有的（x，y）共有3×2个，而满足y=3x 的（x，y）共有一个，由此求得
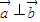的概率．
解答：解：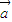
⊥
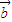等价于 
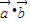=0，即3x-y=0，即 y=3x．
所有的（x，y）共有3×2=6 个，而满足y=3x的（x，y）共有一个（1，3），
故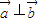
的概率是
，
故答案为
．
点评：本题主要考查古典概型及其概率计算公式的应用，两个向量垂直的性质，属于基础题．
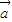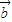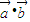⊥ 等价于 =0，即3x-y=0，即 y=3x，所有的（x，y）共有3×2个，而满足y=3x 的（x，y）共有一个，由此求得 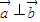的概率．解答：解：
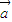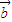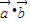⊥ 等价于 =0，即3x-y=0，即 y=3x．所有的（x，y）共有3×2=6 个，而满足y=3x的（x，y）共有一个（1，3），
故
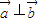的概率是，故答案为
．点评：本题主要考查古典概型及其概率计算公式的应用，两个向量垂直的性质，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知向量
=（-x，1），
=（x，tx），若函数f（x）=
•
在区间[-1，1]上不是单调函数，则实数t的取值范围是（ ）
| a |
| b |
| a |
| b |
| A、（-∞，-2]∪[2，+∞） |
| B、（-∞，-2）∪（2，+∞） |
| C、（-2，2） |
| D、[-2，2] |