题目内容
经过双曲线x2-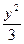 =1的左焦点F1作倾斜角为
=1的左焦点F1作倾斜角为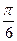 的弦AB,求:
的弦AB,求:
(1)|AB|;
(2)△F2AB的周长(F2为右焦点).
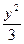 =1的左焦点F1作倾斜角为
=1的左焦点F1作倾斜角为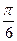 的弦AB,求:
的弦AB,求:(1)|AB|;
(2)△F2AB的周长(F2为右焦点).
1、|AB|=2×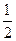 +2=3.
+2=3.
2、△ABF2的周长为3+3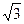 .
.
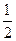 +2=3.
+2=3.2、△ABF2的周长为3+3
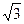 .
.(1)设A(x1,y1),B(x2,y2).直线AB的方程为y=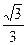 (x+2).
(x+2).
由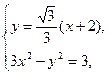 消去y得3x2-
消去y得3x2-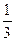 (x+2)2=3,即8x2-4x-13=0,
(x+2)2=3,即8x2-4x-13=0,
∴x1+x2=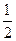 ,x1x2=-
,x1x2=-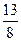 .∴(x1-x2)2=(x1+x2)2-4x1x2=
.∴(x1-x2)2=(x1+x2)2-4x1x2= +
+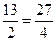 .
.
∴|x1-x2|=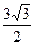 .∴|AB|=
.∴|AB|= ·|x1-x2|=3.
·|x1-x2|=3.
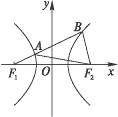
或者:如图,知|AB|=|BF1|-|AF1|,而|BF1|=e(x2+ ),|AF1|=e(-x1-
),|AF1|=e(-x1- ),
),
∴|AB|=e(x1+x2+ )=e(x1+x2)+2a.
)=e(x1+x2)+2a.
∴|AB|=2×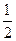 +2=3.
+2=3.
(2)∵|BF2|=e(x2- ),|AF2|=e(
),|AF2|=e( -x1),
-x1),
∴|BF2|+|AF2|=e(x2-x1)=2×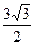 =3
=3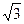 .
.
∴|AB|+|BF2|+|AF2|=3+3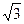 ,故△ABF2的周长为3+3
,故△ABF2的周长为3+3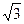 .
.
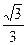 (x+2).
(x+2).
由
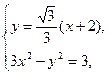 消去y得3x2-
消去y得3x2-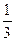 (x+2)2=3,即8x2-4x-13=0,
(x+2)2=3,即8x2-4x-13=0,∴x1+x2=
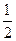 ,x1x2=-
,x1x2=-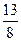 .∴(x1-x2)2=(x1+x2)2-4x1x2=
.∴(x1-x2)2=(x1+x2)2-4x1x2= +
+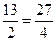 .
.∴|x1-x2|=
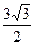 .∴|AB|=
.∴|AB|= ·|x1-x2|=3.
·|x1-x2|=3.或者:如图,知|AB|=|BF1|-|AF1|,而|BF1|=e(x2+
 ),|AF1|=e(-x1-
),|AF1|=e(-x1- ),
),∴|AB|=e(x1+x2+
 )=e(x1+x2)+2a.
)=e(x1+x2)+2a.∴|AB|=2×
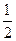 +2=3.
+2=3.(2)∵|BF2|=e(x2-
 ),|AF2|=e(
),|AF2|=e( -x1),
-x1),∴|BF2|+|AF2|=e(x2-x1)=2×
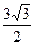 =3
=3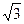 .
.∴|AB|+|BF2|+|AF2|=3+3
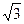 ,故△ABF2的周长为3+3
,故△ABF2的周长为3+3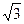 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
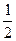 (6-3
(6-3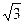 ),求该双曲线的方程.
),求该双曲线的方程.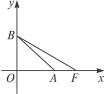
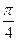 ,
,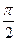 )∪(
)∪(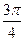 )
) =1上任一点,过P作双曲线两条渐近线的平行线分别交另一条渐近线于Q、R两点,则平行四边形OQPR的面积为…( )
=1上任一点,过P作双曲线两条渐近线的平行线分别交另一条渐近线于Q、R两点,则平行四边形OQPR的面积为…( )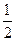 ab
ab
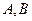 ;
;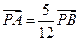 ,求
,求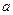 的值.
的值.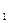 、F
、F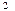 两地听到炮声的时间差为2 s(声速是340m/s),则炮位所在的曲线的轨迹方程是_________。
两地听到炮声的时间差为2 s(声速是340m/s),则炮位所在的曲线的轨迹方程是_________。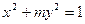 的渐近线过点(-1,2),则该双曲线的虚轴的长是______________。
的渐近线过点(-1,2),则该双曲线的虚轴的长是______________。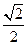 围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数
围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数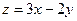 的取值范围为 ( )
的取值范围为 ( ) 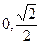 ]
]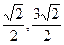 ]
]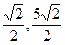 ]
]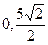 ]
]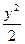 =1的左、右焦点,过F2作垂直于x轴的直线交双曲线于点P,则
=1的左、右焦点,过F2作垂直于x轴的直线交双曲线于点P,则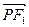 ·
·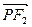 =__________________.
=__________________.