题目内容
如图,OA是双曲线的实半轴,OB是虚半轴,F为焦点,且∠FAB=150°,S△ABF=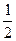 (6-3
(6-3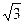 ),求该双曲线的方程.
),求该双曲线的方程.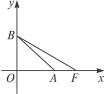
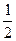 (6-3
(6-3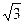 ),求该双曲线的方程.
),求该双曲线的方程.
双曲线方程为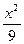 -
-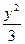 =1.
=1.
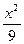 -
-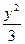 =1.
=1.设双曲线标准方程为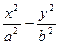 =1.
=1.
A(a,0)、B(0,b)、F(c,0),∠OAB=30°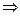 tan30°=
tan30°=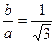
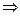 a=
a=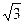 b.
b.
又c2=a2+b2=4b2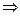 c=2b,
c=2b,
S△=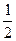 (c-a)b=
(c-a)b=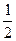 (2-
(2-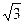 )b2=
)b2=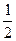 (6-3
(6-3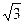 ),∴b2=3,a2=9.
),∴b2=3,a2=9.
∴双曲线方程为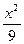 -
-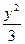 =1.
=1.
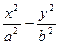 =1.
=1.A(a,0)、B(0,b)、F(c,0),∠OAB=30°
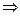 tan30°=
tan30°=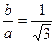
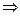 a=
a=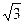 b.
b.又c2=a2+b2=4b2
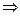 c=2b,
c=2b,S△=
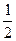 (c-a)b=
(c-a)b=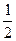 (2-
(2-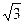 )b2=
)b2=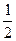 (6-3
(6-3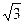 ),∴b2=3,a2=9.
),∴b2=3,a2=9.∴双曲线方程为
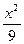 -
-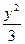 =1.
=1.
练习册系列答案
相关题目
 的距离之比是2∶1的动点P的轨迹方程是_________.
的距离之比是2∶1的动点P的轨迹方程是_________. -
-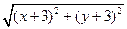 =±4,则动点P的轨迹是( )
=±4,则动点P的轨迹是( )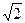 倍,且一个顶点的坐标为(0,2),则双曲线的标准方程为( )
倍,且一个顶点的坐标为(0,2),则双曲线的标准方程为( )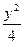 -
-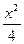 ="1"
="1"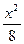 ="1"
="1" 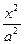 -
-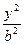 =1上的一点,F为一个焦点,以PF为直径的圆与圆x2+y2=a2的位置关系是( )
=1上的一点,F为一个焦点,以PF为直径的圆与圆x2+y2=a2的位置关系是( )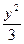 =1的左焦点F1作倾斜角为
=1的左焦点F1作倾斜角为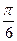 的弦AB,求:
的弦AB,求: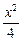 -
-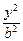 =1(b∈N*)的两个焦点为F1、F2,P为双曲线上一点,|OP|<5,|PF1|、|F1F2|、|PF2|成等差数列,求此双曲线方程.
=1(b∈N*)的两个焦点为F1、F2,P为双曲线上一点,|OP|<5,|PF1|、|F1F2|、|PF2|成等差数列,求此双曲线方程.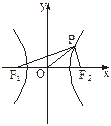
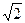 ,则点P的坐标是_________________.
,则点P的坐标是_________________.