Question

【题目】已知抛物线y2=4x的焦点为F，过点F的直线交抛物线于A，B两点． （Ⅰ）若 ，求直线AB的斜率；
（Ⅱ）设点M在线段AB上运动，原点O关于点M的对称点为C，求四边形OACB面积的最小值．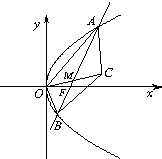

Answer 1

【答案】（Ⅰ）解：依题意F（1，0），设直线AB方程为x=my+1 将直线AB的方程与抛物线的方程联立，消去x得y2﹣4my﹣4=0．
设A（x1 ， y1），B（x2 ， y2），所以 y1+y2=4m，y1y2=﹣4． ①
因为 ，
所以 y1=﹣2y2 ． ②
联立①和②，消去y1 ， y2 ， 得 ．
所以直线AB的斜率是 ．
（Ⅱ）解：由点C与原点O关于点M对称，得M是线段OC的中点，
从而点O与点C到直线AB的距离相等，
所以四边形OACB的面积等于2S△AOB ．
因为
= ，
所以 m=0时，四边形OACB的面积最小，最小值是4．
【解析】（Ⅰ）依题意F（1，0），设直线AB方程为x=my+1．将直线AB的方程与抛物线的方程联立，得y2﹣4my﹣4=0．由此能够求出直线AB的斜率．（Ⅱ）由点C与原点O关于点M对称，得M是线段OC的中点，从而点O与点C到直线AB的距离相等，所以四边形OACB的面积等于2S△AOB ． 由此能求出四边形OACB的面积最小值．