题目内容
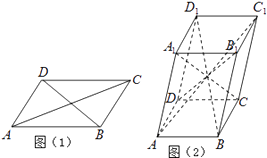
【题目】三棱柱![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,三棱锥
,三棱锥![]() 的体积为
的体积为![]() ,求三棱柱
,求三棱柱![]() 的高.
的高.

【答案】(Ⅰ)证明见解析;(Ⅱ)6.
【解析】解法1:
(Ⅰ)连结![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() .则有
.则有![]() .
.
由题意,可知![]() ,所以
,所以![]() ,
,
所以![]() ,故
,故![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.

(Ⅱ)设三棱柱![]() 的高为
的高为![]() .
.
在![]() 中,
中,
由余弦定理,得![]() ,
,
即![]() ,解得
,解得![]() ,
,
所以![]() 的面积为
的面积为![]() ,
,
由(Ⅰ)可知,点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,
的距离,
所以![]() ,
,
又因为![]() ,
,
所以![]() ,故
,故![]() ,
,
又![]() ,
,
所以![]() ,解得
,解得![]() ,
,
故三棱柱![]() 的高为6.
的高为6.
解法2:(Ⅰ)取![]() 的中点
的中点![]() ,连结
,连结![]() .则有
.则有![]() ,
,
所以四边形![]() 为平形四边形,故
为平形四边形,故![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
由题意,可知![]() ,所以
,所以![]() ,
,
故![]() ∽
∽![]() ,所以
,所以![]() ,
,
又![]() ,故
,故![]() .
.
又![]() ,所以
,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.

(Ⅱ)同解法1.

【题目】某小组共有A、B、C、D、E五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体![]() 名学生中随机抽取了
名学生中随机抽取了![]() 名学生的体检表,并得到如图的频率分布直方图.
名学生的体检表,并得到如图的频率分布直方图.
年级名次 是否近视 |
|
|
近视 |
|
|
不近视 |
|
|
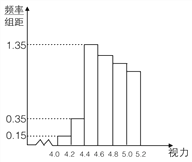
(1)若直方图中后四组的频数成等差数列,试估计全 年级视力在![]() 以下的人数;
以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在![]() 名和
名和![]() 名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过
名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过![]() 的前提下认为视力与学习成绩有关系?
的前提下认为视力与学习成绩有关系?
|
|
|
|
|
|
|
|
|
|
| 7.879 |
![]()
附: