Question

【题目】已知函数其中为常数.

(1)当函数的图象在点处的切线的斜率为1时，求函数在上的最小值； (2)若函数在区间上既有极大值又有极小值，求的取值范围.

Answer 1

【答案】（1）f(x)min＝f(2)＝1－3ln 2.（2）

【解析】【试题分析】（1）依据题设条件，借助导数的几何意义先求参数的值，再运用导数与函数单调性之间的关系求解；（2）利用导函数的零点与函数极值点之间的关系建立不等式组分析求解：

(1)f′(x)＝a＋－ (x>0)，由题意可知，f′＝1，解得a＝1.

故f(x)＝x－－3ln x，∴f′(x)＝，

根据题意由f′(x)＝0，得x＝2.

于是可得下表：

x			2	(2,3)	3
f′(x)		－	0	＋
f(x)			1－3ln 2

∴f(x)min＝f(2)＝1－3ln 2.

(2)f′(x)＝a＋－＝ (x>0),

由题意可得方程ax2－3x＋2＝0有两个不等的正实根，不妨设这两个根为x1，x2，并令h(x)＝ax2－3x＋2，

则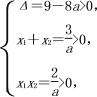

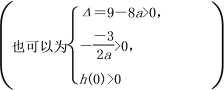
解得0<a<.故a的取值范围为.