题目内容
【题目】以下茎叶图记录了甲，乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊，无法确认，在图中以
表示.
（1）如果
，求乙组同学植树棵数的平均数和方差；
（2）如果
，分别从甲，乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率.（注：方差
，其中
为
， 
，……， 
的平均数）
【答案】（1）
， 
；（2）
.
【解析】试题分析：（1）利用茎叶图中的数据以及平均数与方差的计算公式即可求解；（2）分别列出所有基本事件以及符合题意的基本事件的种数，利用古典概型即可求解.
试题解析：（1）当
时，由茎叶图可知，乙组同学的植树棵数是
，，
，
，
∴平均数
，方差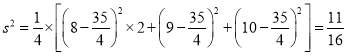
；
（2）记甲组四名同学分别为
， 
， 
， 
，他们植树的棵数依次为，， 
， 
；乙组四名同学分别为
， 
， 
， 
，他们植树的棵数依次为，，，，分别从甲、乙两组中随机选取一名同学，所有可能的结果有
个，即
， 
， 
， 
， 
， 
， 
，
， 
， 
， 
， 
， 
， 
， 
， 
，
用
表示“选出的两名同学的植树总棵数为
”这一事件，则
中的结果有
个，它们是
， 
， 
， 
，故所示概率
.
【题目】已知函数
的定义域为[-1,5]，部分对应值如下表，的导函数
的图象如图所示，下列关于的命题：
| -1 | 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
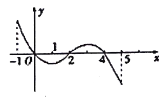
①函数的极大值点为0,4；
②函数在[0,2]上是减函数；
③如果当
时，的最大值是2，那么
的最大值为4；
④当
时，函数
有4个零点.
其中正确命题的序号是__________．
【题目】某房屋开发公司根据市场调查，计划在2017年开发的楼盘中设计“特大套”、“大套”、“经济适
用房”三类商品房,每类房型中均有舒适和标准两种型号.某年产量如下表:
房型 | 特大套 | 大套 | 经济适用房 |
舒适 | 100 | 150 |
|
标准 | 300 |
| 600 |
若按分层抽样的方法在这一年生产的套房中抽取50套进行检测,则必须抽取“特大套”套房10套, “大套”15套.
(1)求
,
的值;
(2)在年终促销活动中,奖给了某优秀销售公司2套舒适型和3套标准型“经济适用型”套房，该销售公司又从中随机抽取了2套作为奖品回馈消费者.求至少有一套是舒适型套房的概率;
(3)今从“大套”类套房中抽取6套,进行各项指标综合评价,并打分如下:
现从上面6个分值中随机的一个一个地不放回抽取,规定抽到数9.6或9.7,抽取工作即停止.记在抽取到数9.6或9.7所进行抽取的次数为
,求的分布列及数学期望.
