题目内容
【题目】在一次水下考古活动中,某一潜水员需潜水![]() 米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为
米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为![]() 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为![]() 升;②水底作业时间范围是最少
升;②水底作业时间范围是最少![]() 分钟最多
分钟最多![]() 分钟,每分钟用氧量为
分钟,每分钟用氧量为![]() 升;③返回水面时,平均速度为
升;③返回水面时,平均速度为![]() 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为![]() 升.潜水员在此次考古活动中的总用氧量为
升.潜水员在此次考古活动中的总用氧量为![]() 升.
升.
(1)如果水底作业时间是![]() 分钟,将
分钟,将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,水底作业时间为
,水底作业时间为![]() 分钟,求总用氧量
分钟,求总用氧量![]() 的取值范围;
的取值范围;
(3)若潜水员携带氧气![]() 升,请问潜水员最多在水下多少分钟(结果取整数)?
升,请问潜水员最多在水下多少分钟(结果取整数)?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)通过速度、时间与路程之间的关系可知下潜所需时间为![]() 分钟、返回所需时间为
分钟、返回所需时间为![]() 分钟,进而列式可得结论;(2)由(1)知
分钟,进而列式可得结论;(2)由(1)知![]() ,由对勾函数的单调性可得
,由对勾函数的单调性可得![]() 的取值范围是
的取值范围是![]() ;(3)由题意知潜水与返回最少要用
;(3)由题意知潜水与返回最少要用![]() 升氧气,可得在水下时间最长为
升氧气,可得在水下时间最长为![]() .
.
试题解析:(1)依题意下潜时间![]() 分钟,返回时间
分钟,返回时间![]() 分钟,
分钟,
![]()
整理得![]() .
.
(2)由(1)同理得![]()
函数在![]() 是减函数,
是减函数,![]() 是增函数
是增函数
当![]() 时
时![]() ,当
,当![]() 时
时![]() ,
,![]() 时
时![]()
所以总用氧量![]() 的取值范围是
的取值范围是![]() .
.
(3)潜水员在潜水与返回最少要用![]() 升氧气,则在水下时间最长为
升氧气,则在水下时间最长为![]() 分钟
分钟
所以潜水员最多在水下![]() 分钟.
分钟.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某企业生产的一种产品的广告费用![]() (单位:万元)与销售额
(单位:万元)与销售额![]() (单位:万元)的统计数据如下表:
(单位:万元)的统计数据如下表:
广告费用 |
|
|
|
|
|
销售额 |
|
|
|
|
|
(1)根据上述数据,求出销售额![]() (万元)关于广告费用
(万元)关于广告费用![]() (万元)的线性回归方程;
(万元)的线性回归方程;
(2)如果企业要求该产品的销售额不少于![]() 万元,则投入的广告费用应不少于多少万元?
万元,则投入的广告费用应不少于多少万元?
(参考数值: ![]() .
.
回归直线的斜率和截距的最小二乘法估计公式分别为: 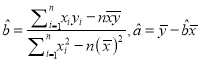 )
)