题目内容
【题目】已知三棱柱ABC﹣A1B1C1中,侧面ABB1A1为正方形,延长AB到D,使得AD=BD,平面AA1C1C⊥平面ABB1A1 , A1C1= ![]() AA1 , ∠C1A1A=
AA1 , ∠C1A1A= ![]() .
. 
(1)若E,F分别为C1B1 , AC的中点,求证:EF∥平面ABB1A1;
(2)求平面A1B1C1与平面CB1D所成的锐二面角的余弦值.
【答案】
(1)证明:取A1C1的中点G,连结FG,EG,
在△A1B1C1中,EG为中位线,∴EG∥A1B1,
∴GE平面ABB1A1,A1B1平面ABB1A1,
∴GE∥ABB1A1,同理得GF∥平面ABB1A1,
又GF∩GE=G,∴平面GEF∥平面ABB1A1,
∵EF平面GEF,∴EF∥平面ABB1A1.
(2)解:连结AC1,在△AA1C1中, ![]() ,
, ![]() ,
,
∴由余弦定理得 ![]() =
= ![]() +
+ ![]() ﹣2AA1×A1C1cos∠AA1C1=
﹣2AA1×A1C1cos∠AA1C1= ![]() ,
,
∴AA1=AC1,△A1AC1是等腰直角三角形,AC1⊥AA1,
又∵平面AA1C1C∩平面ABB1A1=AA1,
∴AC1⊥平面ABB1A1,
∵AB平面ABB1A1,∴AC1⊥AB,
又∵侧面ABB1A1为正方形,∴AA1⊥AB,
分别以AA1,AB,AC1所在直线为x轴,y轴,z轴,建立空间直角坐标系,
设AB=1,则A(0,0,0),A1(1,0,0),B1(1,1,0),
C1(0,0,1),C(﹣1,0,1),D(0,2,0),
∴ ![]() =(2,1,﹣1),
=(2,1,﹣1), ![]() =(1,2,﹣1),
=(1,2,﹣1), ![]() =(﹣1,0,1),
=(﹣1,0,1), ![]() =(0,1,0),
=(0,1,0),
设平面A1B1C1的法向量 ![]() =(x,y,z),
=(x,y,z),
则 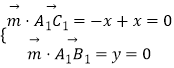 ,取x=1,得
,取x=1,得 ![]() =(1,0,1),
=(1,0,1),
设平面CB1D的法向量 ![]() =(a,b,c),
=(a,b,c),
则 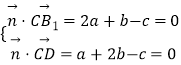 ,取a=1,得
,取a=1,得 ![]() =(1,1,3),
=(1,1,3),
cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
∴平面A1B1C1与平面CB1D所成的锐二面角的余弦值为 ![]() .
.

【解析】(1)取A1C1的中点G,连结FG,EG,则EG∥A1B1 , 从而GE∥ABB1A1 , 同理得GF∥平面ABB1A1 , 从平面GEF∥平面ABB1A1 , 由此能证明EF∥平面ABB1A1 . (2)连结AC1 , 推导出AC1⊥AA1 , 从而AC1⊥平面ABB1A1 , 再求出AC1⊥AB,AA1⊥AB,分别以AA1 , AB,AC1所在直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出平面A1B1C1与平面CB1D所成的锐二面角的余弦值.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。
