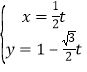题目内容
【题目】将函数f(x)=3sin(4x+ ![]() )图象上所有点的横坐标伸长到原来的2倍,再向右平移
)图象上所有点的横坐标伸长到原来的2倍,再向右平移 ![]() 个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
A.x= ![]()
B.x= ![]()
C.![]()
D.![]()
【答案】C
【解析】解:将函数f(x)=3sin(4x+ ![]() )图象上所有点的横坐标伸长到原来的2倍,可得函数y=3sin(2x+
)图象上所有点的横坐标伸长到原来的2倍,可得函数y=3sin(2x+ ![]() )的图象,
)的图象,
再向右平移 ![]() 个单位长度,可得y=3sin[2(x﹣
个单位长度,可得y=3sin[2(x﹣ ![]() )+
)+ ![]() ]=3sin(2x﹣
]=3sin(2x﹣ ![]() )的图象,故g(x)=3sin(2x﹣
)的图象,故g(x)=3sin(2x﹣ ![]() ).
).
令 2x﹣ ![]() =kπ+
=kπ+ ![]() ,k∈z,得到 x=
,k∈z,得到 x= ![]() π+
π+ ![]() ,k∈z.
,k∈z.
则得 y=g(x)图象的一条对称轴是 ![]() ,
,
故选:C.
【考点精析】根据题目的已知条件,利用正弦函数的对称性和函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握正弦函数的对称性:对称中心![]() ;对称轴
;对称轴![]() ;图象上所有点向左(右)平移
;图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目