题目内容
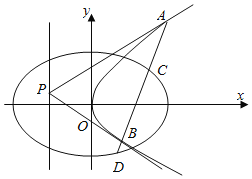
【题目】若给定椭圆![]() 和点
和点![]() ,则称直线
,则称直线![]() 为椭圆C的“伴随直线”.
为椭圆C的“伴随直线”.
(1)若![]() 在椭圆C上,判断椭圆C与它的“伴随直线”的位置关系(当直线与椭圆的交点个数为0个、1个、2个时,分别称直线与椭圆相离、相切、相交),并说明理由;
在椭圆C上,判断椭圆C与它的“伴随直线”的位置关系(当直线与椭圆的交点个数为0个、1个、2个时,分别称直线与椭圆相离、相切、相交),并说明理由;
(2)命题:“若点![]() 在椭圆C的外部,则直线
在椭圆C的外部,则直线![]() 与椭圆C必相交.”写出这个命题的逆命题,判断此逆命题的真假,说明理由;
与椭圆C必相交.”写出这个命题的逆命题,判断此逆命题的真假,说明理由;
(3)若![]() 在椭圆C的内部,过N点任意作一条直线,交椭圆C于A、B,交
在椭圆C的内部,过N点任意作一条直线,交椭圆C于A、B,交![]() 于M点(异于A、B),设
于M点(异于A、B),设![]() ,问
,问![]() 是否为定值?说明理由.
是否为定值?说明理由.
【答案】(1)l与椭圆C相切.见解析(2)逆命题:若直线![]() 与椭圆C相交,则点
与椭圆C相交,则点![]() 在椭圆C的外部.是真命题.见解析(3)为定值0,见解析
在椭圆C的外部.是真命题.见解析(3)为定值0,见解析
【解析】
(1) 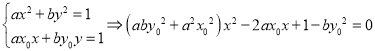 ,由根的差别式能得到l与椭圆C相切.
,由根的差别式能得到l与椭圆C相切.
(2)逆命题:若直线![]() 与椭圆C相交,则点
与椭圆C相交,则点![]() 在椭圆C的外部.是真命题.联立方程得
在椭圆C的外部.是真命题.联立方程得![]() .由
.由![]() ,能求出
,能求出![]() 在椭圆C的外部.
在椭圆C的外部.
(3)此时![]() 与椭圆相离,设
与椭圆相离,设![]() 则
则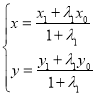 代入椭圆
代入椭圆![]() ,利用M在
,利用M在![]() 上,得
上,得![]() .由此能求出
.由此能求出![]() .
.
解:(1)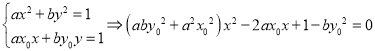
即![]()
∴![]()
∴![]() 与椭圆C相切.
与椭圆C相切.
(2)逆命题:若直线![]() 与椭圆C相交,
与椭圆C相交,
则点![]() 在椭圆C的外部.
在椭圆C的外部.
是真命题.联立方程得![]()
则![]()
∴![]()
∴![]()
∴![]() 在椭圆C的外部.
在椭圆C的外部.
(3)同理可得此时![]() 与椭圆相离,设
与椭圆相离,设![]()
则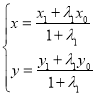 代入椭圆
代入椭圆![]() ,利用M在
,利用M在![]() 上,
上,
即![]() ,整理得
,整理得![]()
同理得关于![]() 的方程,类似.
的方程,类似.
即![]() 是
是![]() 的两根
的两根
∴![]() .
.

【题目】某校为调查学生喜欢“应用统计”课程是否与性别有关,随机抽取了选修课程的55名学生,得到数据如下表:
喜欢统计课程 | 不喜欢统计课程 | ||
男生 | 20 | 5 | |
女生 | 10 | 20 | |
(1)判断是否有99.5%的把握认为喜欢“应用统计”课程与性别有关?
(2)用分层抽样的方法从喜欢统计课程的学生中抽取6名学生作进一步调查,将这6名学生作为一个样本,从中任选2人,求恰有1个男生和1个女生的概率.
临界值参考:
| 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
(2)已知在被调查的女生中有5名数学系的学生,其中3名对冰球有兴趣,现在从这5名学生中随机抽取3人,求至少有2人对冰球有兴趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()