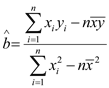Question

【题目】在矩形ABCD中，AB＝1，AD＝2，动点P在以点C为圆心且与BD相切的圆上．若＝λ＋μ，则λ＋μ的最大值为(　　)

A. 3 B. 2

C. D. 2

Answer 1

【答案】A

【解析】建立如图所示的直角坐标系，则C点坐标为(2,1)．

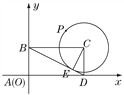
设BD与圆C切于点E，连接CE，则CE⊥BD.

∵ CD＝1，BC＝2，

∴ BD＝，

EC，

即圆C的半径为，

∴ P点的轨迹方程为(x－2)2＋(y－1)2＝.

设P(x0，y0)，则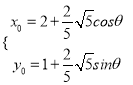 (θ为参数)，

而＝(x0，y0)， ＝(0,1)， ＝(2,0)．

∵＝λ＋μ＝λ(0,1)＋μ(2,0)＝(2μ，λ)，

∴ μ＝x0＝1＋cos θ，λ＝y0＝1＋sin θ.

两式相加，得λ＋μ＝1＋sin θ＋1＋cos θ＝2＋sin(θ＋φ)≤3

当且仅当θ＝＋2kπ－φ，k∈Z时，λ＋μ取得最大值3.

故选A.