Question

【题目】设函数 (k为常数，e＝2.718 28…是自然对数的底数).

(1)当k≤0时，求函数f (x)的单调区间；

(2)若函数f (x)在(0，2)内存在两个极值点，求k的取值范围.

Answer 1

【答案】（1）见解析；（2）

【解析】试题分析：（1）定义域为(0，＋∞)，求单调区间，先求导，并因式分解得，由于k≤0，所以，只有一解x=2.

(2)由(1)知，k≤0时，函数f (x)在(0，2)内单调递减，故f (x)在(0，2)内不存在极值点；

再考虑k>0时， ，由于，只需分析g(x)＝ex－kx，x∈[0，＋∞)的零点情况。对g(x)求导分析，g′(x)＝ex－k＝ex－eln k，再分0＜k≤1和k＞1讨论即可求。

试题解析：

函数y＝f (x)的定义域为(0，＋∞).

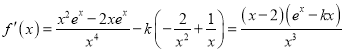
由k≤0可得ex－kx＞0，

所以当x∈(0，2)时，f′(x)＜0，函数y＝f (x)单调递减，

x∈(2，＋∞)时，f′(x)＞0，函数y＝f (x)单调递增.

所以f (x)的单调递减区间为(0，2)，单调递增区间为(2，＋∞).

(2)由(1)知，k≤0时，函数f (x)在(0，2)内单调递减，

故f (x)在(0，2)内不存在极值点；

当k＞0时，设函数g(x)＝ex－kx，x∈[0，＋∞).

因为g′(x)＝ex－k＝ex－eln k，当0＜k≤1时，

当x∈(0，2)时，g′(x)＝ex－k＞0，y＝g(x)单调递增.

故f (x)在(0，2)内不存在两个极值点；

当k＞1时，得x∈(0，ln k)时，g′(x)＜0，函数y＝g(x)单调递减.

x∈(ln k，＋∞)时，g′(x)＞0，函数y＝g(x)单调递增.

所以函数y＝g(x)的最小值为g(ln k)＝k(1－ln k).

函数f (x)在(0，2)内存在两个极值点当且仅当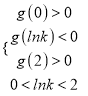解得e＜k＜，

综上所述，函数f (x)在(0，2)内存在两个极值点时，k的取值范围为.