题目内容
19.已知数列{an}满足a1=2,n≥2时,an=22nan-1+n•2${\;}^{{n}^{2}}$,求数列{an}的通项公式.分析 通过对等式an=22nan-1+n•2${\;}^{{n}^{2}}$两边同时除以${2}^{{n}^{2}+1}$可知$\frac{{a}_{n}}{{2}^{n•(n+1)}}$=$\frac{{a}_{n-1}}{{2}^{(n-1)•n}}$+$\frac{n}{2}$,利用累加法计算即得结论.
解答 解:∵an=22nan-1+n•2${\;}^{{n}^{2}}$,
∴$\frac{{a}_{n}}{{2}^{{n}^{2}+1}}$=$\frac{{2}^{2n}{a}_{n-1}+n•{2}^{{n}^{2}}}{{2}^{{n}^{2}+1}}$,
整理得:$\frac{{a}_{n}}{{2}^{n•(n+1)}}$=$\frac{{a}_{n-1}}{{2}^{(n-1)•n}}$+$\frac{n}{2}$,
∴$\frac{{a}_{n-1}}{{2}^{(n-1)•n}}$=$\frac{{a}_{n-2}}{{2}^{(n-2)•(n-1)}}$+$\frac{n-1}{2}$,
…
$\frac{{a}_{2}}{{2}^{2•3}}$=$\frac{{a}_{1}}{{2}^{1•2}}$+$\frac{2}{2}$,
累加得:$\frac{{a}_{n}}{{2}^{n•(n+1)}}$$\frac{{a}_{1}}{{2}^{1•2}}$+$\frac{2}{2}$+$\frac{3}{2}$+…+$\frac{n}{2}$
=$\frac{1}{2}$+$\frac{2}{2}$+$\frac{3}{2}$+…+$\frac{n}{2}$
=$\frac{1}{2}$•$\frac{n(n+1)}{2}$
=$\frac{n(n+1)}{{2}^{2}}$,
∴an=2n(n+1)•$\frac{n(n+1)}{{2}^{2}}$=n(n+1)•${2}^{{n}^{2}+n-2}$.
点评 本题考查数列的通项,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

| A. | 若y=f(x)是减函数,则f′(x)<0 | |
| B. | 若△ABC为锐角三角形,则sinA+sinB>cosA+cosB | |
| C. | 因为a>b(a,b∈R),则a+2i>b+2i | |
| D. | 在平面直角坐标系中,若两直线平行,则它们的斜率相等 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
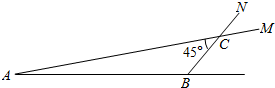 如图,小明、小王分别从A点处和B点处同时出发,小明乘公交沿着AM方向行走,车速为36km/h,小王骑自行车沿着BN方向行走,10min后,两人在公交站C点处相遇.已知,小王此时骑车行程为BC=(3$\sqrt{2}$-$\sqrt{6}$)km,两人出行方向夹角∠ACB=45°,求两人出发前的距离AB为多少km?
如图,小明、小王分别从A点处和B点处同时出发,小明乘公交沿着AM方向行走,车速为36km/h,小王骑自行车沿着BN方向行走,10min后,两人在公交站C点处相遇.已知,小王此时骑车行程为BC=(3$\sqrt{2}$-$\sqrt{6}$)km,两人出行方向夹角∠ACB=45°,求两人出发前的距离AB为多少km?