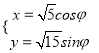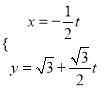Question

【题目】对于定义在D上的函数f（x），若存在距离为d的两条直线y=kx+m1和y=kx+m2 ， 使得对任意x∈D都有kx+m1≤f（x）≤kx+m2恒成立，则称函数f（x）（x∈D）有一个宽度为d的通道．给出下列函数： ①f（x）= ；
②f（x）=sinx；
③f（x）= ；
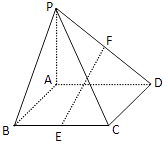
④f（x）=
其中在区间[1，+∞）上通道宽度可以为1的函数有（写出所有正确的序号）．

Answer 1

【答案】①③④
【解析】解：函数①，在区间[1，+∞）上的值域为（0，1]， 满足0≤f（x）≤1，
∴该函数在区间[1，+∞）上通道宽度可以为1；
函数②，在区间[1，+∞）上的值域为[﹣1，1]，
满足﹣1≤f（x）≤1，
∴该函数在区间[1，+∞）上通道宽度可以为2；
函数③，在区间[1，+∞）上的图象是双曲线x2﹣y2=1在第一象限的部分，
其渐近线为y=x，满足x﹣1≤f（x）≤x，
∴该函数在区间[1，+∞）上通道宽度可以为1；
函数④，在区间[1，+∞）上的值域为[0， ]，
满足0≤f（x）≤ 1，
∴该函数在区间[1，+∞）上通道宽度可以为1．
故满足题意的有①③④．
所以答案是①③④．