题目内容
【题目】设等差数列{an}中,a2=-8,a6=0.
(1)求数列{an}的通项公式;
(2)若等比数列{bn}满足b1=-8,b2=a1+a2+a3,求数列{bn}的前n项和Sn.
【答案】(1)an=2n-12,n∈N*;(2)![]() ,n∈N*.
,n∈N*.
【解析】
(1)等差数列{an}的公差设为d,运用等差数列的通项公式,可列方程为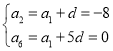 ,解方程可得首项和公差,进而得到所求通项公式;
,解方程可得首项和公差,进而得到所求通项公式;
(2)等比数列{bn}的公比设为q,由(1)可得![]() ,可得公比q,再由等比数列的求和公式求解即可
,可得公比q,再由等比数列的求和公式求解即可
解:(1)等差数列{an}的公差设为d,![]() ,a6=0,
,a6=0,
可得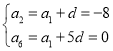 ,解得
,解得![]() ,
,
则![]() ,n∈N*
,n∈N*
(2)等比数列{bn}的公比设为q,![]() ,
,
由(1)可得,![]() ,则q=
,则q=![]() =3,
=3,
所以前n项和Sn=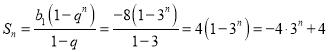 ,n∈N*
,n∈N*

练习册系列答案
相关题目
【题目】某校2011年到2019年参加“北约”“华约”考试而获得加分的学生人数(每位学生只能参加“北约”“华约”中的一种考试)可以通过以下表格反映出来,(为了方便计算,将2011年编号为1,2012年编号为2,依此类推)
年份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数y | 2 | 3 | 5 | 4 | 5 | 7 | 8 | 10 | 10 |
(1)求这九年来,该校参加“北约”“华约”考试而获得加分的学生人数的平均数和方差;
(2)根据最近五年的数据,利用最小二乘法求出y与x的线性回归方程,并依此预测该校2020年参加“北约”“华约”考试而获得加分的学生人数.(最终结果精确至个位)
参考数据:回归直线的方程是![]() ,其中
,其中 ,
,![]() ,
,![]() ,
,![]() .
.