题目内容
【题目】如图所示,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分别为线段AD,PC的中点.
AD,E,F分别为线段AD,PC的中点.
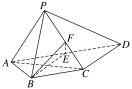
(1)求证:AP∥平面BEF;
(2)求证:BE⊥平面PAC.
【答案】 (1) 证明见解析
(2) 证明见解析
【解析】
(1)连接CE,OF,易知四边形ABCE是菱形,可得O是AC的中点,利用中位线的概念,可得PA∥OF,从而可证AP∥平面BEF;
(2)通过证明AP⊥BE、BE⊥AC,可证明BE⊥平面PAC
证明: (1)如图所示,设AC∩BE=O,连接OF,EC.
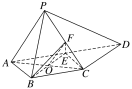
由于E为AD的中点,AB=BC=![]() AD,AD∥BC,
AD,AD∥BC,
所以AE∥BC,且AE=AB=BC,因此,四边形ABCE为菱形,
所以O为AC的中点.又F为PC的中点,
所以在△PAC中,可得AP∥OF.
又OF![]() 平面BEF,AP
平面BEF,AP![]() 平面BEF,
平面BEF,
所以AP∥平面BEF.
(2)由题意,知ED∥BC,ED=BC,
所以四边形BCDE为平行四边形,所以BE∥CD.
又AP⊥平面PCD,所以AP⊥CD,所以AP⊥BE.
因为四边形ABCE为菱形,所以BE⊥AC.
又AP∩AC=A,AP,AC![]() 平面PAC,
平面PAC,
所以BE⊥平面PAC

【题目】为弘扬中华传统文化,学校课外阅读兴趣小组进行每日一小时的“经典名著”和“古诗词”的阅读活动. 根据调查,小明同学阅读两类读物的阅读量统计如下:
小明阅读“经典名著”的阅读量![]() (单位:字)与时间t(单位:分钟)满足二次函数关系,部分数据如下表所示;
(单位:字)与时间t(单位:分钟)满足二次函数关系,部分数据如下表所示;
t | 0 | 10 | 20 | 30 |
| 0 | 2700 | 5200 | 7500 |
阅读“古诗词”的阅读量![]() (单位:字)与时间t(单位:分钟)满足如图1所示的关系.
(单位:字)与时间t(单位:分钟)满足如图1所示的关系.

(1)请分别写出函数![]() 和
和![]() 的解析式;
的解析式;
(2)在每天的一小时课外阅读活动中,小明如何分配“经典名著”和“古诗词”的阅读时间,使每天的阅读量最大,最大值是多少?


