题目内容
4.已知f(x)是定义在R上的函数,且f(x)=$\frac{1+f(x-2)}{1-f(x-2)}$,若f(2)=2+$\sqrt{3}$,则f(2006)=$\sqrt{3}-2$.分析 根据条件f(x)=$\frac{1+f(x-2)}{1-f(x-2)}$,得到函数f(x)是周期为8的周期函数,进行转化求解即可.
解答 解:∵f(x)=$\frac{1+f(x-2)}{1-f(x-2)}$,
∴f(x-2)=$\frac{1+f(x-4)}{1-f(x-4)}$,
∴f(x)=$\frac{1+\frac{1+f(x-4)}{1-f(x-4)}}{1-\frac{1+f(x-4)}{1-f(x-4)}}$=-$\frac{1}{f(x-4)}$,
即f(x-4)=-$\frac{1}{f(x-8)}$
∴f(x)=f(x-8),
即函数f(x)是周期为8的周期函数,
则f(2006)=f(250×8+6)=f(6),
∵f(2)=2+$\sqrt{3}$,
∴f(4)=$\frac{1+f(2)}{1-f(2)}$=$\frac{1+2+\sqrt{3}}{1-2-\sqrt{3}}$=$\frac{3+\sqrt{3}}{-1-\sqrt{3}}$=-$\sqrt{3}$,
f(6)=$\frac{1+f(4)}{1-f(4)}=\frac{1-\sqrt{3}}{1+\sqrt{3}}$=$\sqrt{3}-2$,
即f(2006)=$\sqrt{3}-2$,
故答案为:$\sqrt{3}-2$.
点评 本题主要考查函数值的计算,根据条件判断函数的周期性是解决本题的关键.

练习册系列答案
相关题目
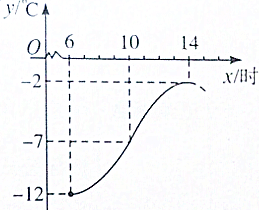 如图,牡丹江市某天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ<π|).
如图,牡丹江市某天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ<π|).