题目内容
14.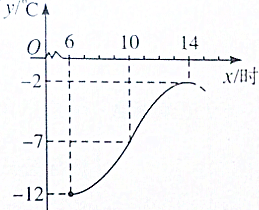 如图,牡丹江市某天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ<π|).
如图,牡丹江市某天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ<π|).(1)求这段时间最大温差;
(2)求这段曲线的函数解析式.
分析 (1)由图易知,这段时间的最高气温为-2℃,最低气温为-12℃,从而得解;
(2)从6时到14时的图象是函数y=Asin(ωx+φ)+b的半个周期的图象,从而可得A,ω,φ,b的值.
解答 解:(1)由题中图所知,这段时间的最高气温为-2℃,最低气温为-12℃,故这段时间最大温差为-2-(-12)=10℃.…(4分)
(2)从6时到14时的图象是函数y=Asin(ωx+φ)+b的半个周期的图象,
所以$\frac{1}{2}$T=$\frac{1}{2}$•$\frac{2π}{ω}$=14-6,得ω=$\frac{π}{8}$…(7分)
A=$\frac{1}{2}$(-2+12)=5,…(9分)
b=$\frac{1}{2}$(-2-12)=-7,…(11分)
这时y=5sin($\frac{π}{8}$x+φ)-7,将x=6,y=-12代入上式,
可得φ=$\frac{3π}{4}$,
综上可得:y=5sin($\frac{π}{8}$x+$\frac{3π}{4}$)-7.…(13分)
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,熟练应用函数的最值求A与b是关键,属于中档题.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
10.不等式x2+ax+b<0的解集是(-1,3),则( )
| A. | $\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=1}\\{b=-6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$ |
2. 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )
 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )| A. | $\frac{1}{8}$ | B. | 8 | C. | 9 | D. | $\frac{1}{9}$ |
6.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了四次试验如下:
(1)求y关于x的线性回归方程
(2)试预测加工10个零件需要多少时间?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$ $\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 零件的个数x/个 | 2 | 3 | 4 | 5 |
| 加工的时间y/小时 | 2.5 | 3 | 4 | 4.5 |
(2)试预测加工10个零件需要多少时间?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$ $\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
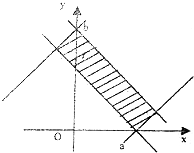 设满足y≥|x-a|的点(x,y)的集合为A,满足y≤-|x|+b的点(x,y)的集合为B,其中a、b是正数,且A∩B≠∅.
设满足y≥|x-a|的点(x,y)的集合为A,满足y≤-|x|+b的点(x,y)的集合为B,其中a、b是正数,且A∩B≠∅.