题目内容
已知数列 满足
满足 ,
, 我们知道当a取不同的值时,得到不同的数列,如当
我们知道当a取不同的值时,得到不同的数列,如当 时,得到无穷数列:
时,得到无穷数列: 当
当 时,得到有穷数列:
时,得到有穷数列: .
.
(Ⅰ)求当 为何值时
为何值时 ;
;
(Ⅱ)设数列 满足
满足 ,
,  ,求证:
,求证: 取数列
取数列 中的任一个数,都可以得到一个有穷数列
中的任一个数,都可以得到一个有穷数列 ;
;
(Ⅲ)若 ,求
,求 的取值范围.
的取值范围.
 满足
满足 ,
, 我们知道当a取不同的值时,得到不同的数列,如当
我们知道当a取不同的值时,得到不同的数列,如当 时,得到无穷数列:
时,得到无穷数列: 当
当 时,得到有穷数列:
时,得到有穷数列: .
.(Ⅰ)求当
 为何值时
为何值时 ;
;(Ⅱ)设数列
 满足
满足 ,
,  ,求证:
,求证: 取数列
取数列 中的任一个数,都可以得到一个有穷数列
中的任一个数,都可以得到一个有穷数列 ;
;(Ⅲ)若
 ,求
,求 的取值范围.
的取值范围.(Ⅰ)当 为
为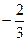 何值时
何值时
(Ⅱ)证明略
(Ⅲ)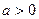
 为
为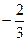 何值时
何值时
(Ⅱ)证明略
(Ⅲ)
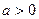
(Ⅰ)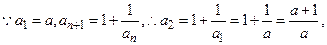
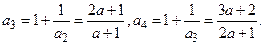
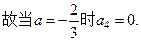
(Ⅱ) 解法一: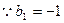 ,
,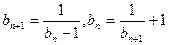 ,
,
当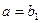 时,
时,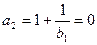 ,
,
当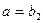 时,
时,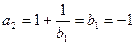 ,
,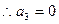 ,
,
当 时,
时,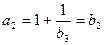 ,
,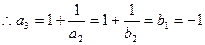
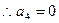 .
.
一般地, 当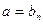 时,
时,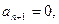 可得一个含有
可得一个含有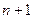 项的有穷数列
项的有穷数列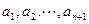 .
.
下面用数学归纳法证明.
(1)当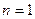 时,
时, 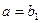 ,显然
,显然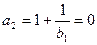 ,可得一个含有2项的有穷数列
,可得一个含有2项的有穷数列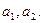
(2)假设当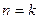 时,
时,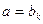 ,得到一个含有
,得到一个含有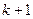 项的有穷数列
项的有穷数列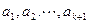 ,其中
,其中
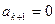 ,则
,则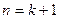 时,
时,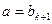 ,
,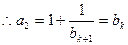 ,
,
由假设可知,得到一个含有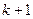 项的有穷数列
项的有穷数列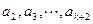 ,其中
,其中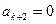 .
.
所以,当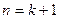 时, 可以得到一个含有
时, 可以得到一个含有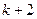 项的有穷数列
项的有穷数列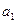 ,
,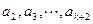 ,其中
,其中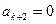
由(1),(2)知,对一切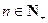 ,命题都成立.
,命题都成立.
解法二: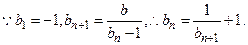
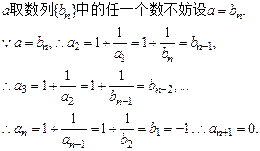
故 取数列
取数列 中的任一个数,都可以得到一个有穷数列
中的任一个数,都可以得到一个有穷数列 .
.
(Ⅲ) 即
即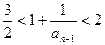 ,
,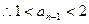
所以要使 ,当且仅当它的前一项
,当且仅当它的前一项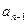 满足
满足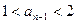 .
.
由于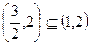 ,所以只须当
,所以只须当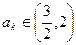 时,都有
时,都有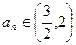
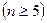
 由
由 ,得
,得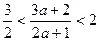 , 解得
, 解得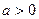 .
.
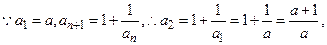
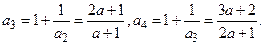
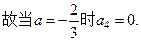
(Ⅱ) 解法一:
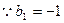 ,
,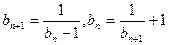 ,
,当
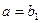 时,
时,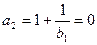 ,
,当
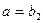 时,
时,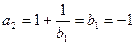 ,
,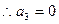 ,
,当
 时,
时,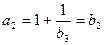 ,
,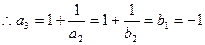
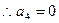 .
.一般地, 当
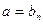 时,
时,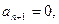 可得一个含有
可得一个含有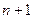 项的有穷数列
项的有穷数列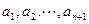 .
.下面用数学归纳法证明.
(1)当
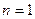 时,
时, 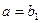 ,显然
,显然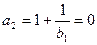 ,可得一个含有2项的有穷数列
,可得一个含有2项的有穷数列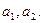
(2)假设当
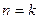 时,
时,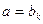 ,得到一个含有
,得到一个含有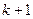 项的有穷数列
项的有穷数列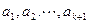 ,其中
,其中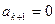 ,则
,则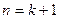 时,
时,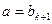 ,
,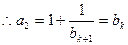 ,
,由假设可知,得到一个含有
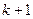 项的有穷数列
项的有穷数列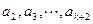 ,其中
,其中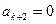 .
.所以,当
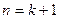 时, 可以得到一个含有
时, 可以得到一个含有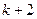 项的有穷数列
项的有穷数列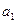 ,
,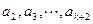 ,其中
,其中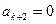
由(1),(2)知,对一切
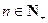 ,命题都成立.
,命题都成立.解法二:
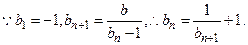
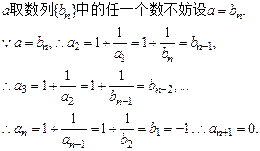
故
 取数列
取数列 中的任一个数,都可以得到一个有穷数列
中的任一个数,都可以得到一个有穷数列 .
.(Ⅲ)
 即
即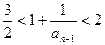 ,
,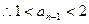
所以要使
 ,当且仅当它的前一项
,当且仅当它的前一项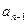 满足
满足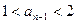 .
.由于
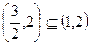 ,所以只须当
,所以只须当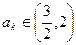 时,都有
时,都有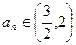
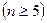
 由
由 ,得
,得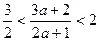 , 解得
, 解得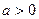 .
.
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 ,
, ,
, ,
, ,求数列
,求数列 ,
, 通项公式
通项公式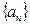 满足
满足 ,
,
 ,求
,求 .
. 中,
中, ,求
,求 ,并归纳出
,并归纳出 .
.


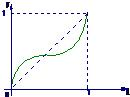
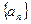 中,
中, ,求
,求 取最小值时
取最小值时 的值.
的值. 的前
的前 项和
项和 ,求
,求