题目内容
在等比数列{an}中,已知a3=
,S3=
.
(1)求{an}的通项公式;
(2)求和Sn=a1+2a2+…+nan.
| 3 |
| 2 |
| 9 |
| 2 |
(1)求{an}的通项公式;
(2)求和Sn=a1+2a2+…+nan.
(1)由条件得:a1q2=
,(1分)
a1+a1q+a1q2=
,(2分)
∴
=2(3分)
∴q=1或q=-
(4分)
当q=1时,a1=
,an=
(5分)
当q=-
时,a1=6,an=6(-
)n-1(6分)
所以当q=1时,an=
;当q=-
时,an=6(-
)n-1.(7分)
(2)当q=1时,Sn=
(1+2+…+n)=
;(9分)
当q=-
时,Sn=6[(-
)0+2×(-
)1+3×(-
)2+…+n(-
)n-1](10分)
∴-
Sn=6[(-
)1+2×(-
)2+3×(-
)3+…+n(-
)n](11分)
∴
Sn=6[1+(-
)+(-
)2+…+(-
)n-1-n(-
)n](12分)
=6[
-n(-
)n](13分)
∴Sn=
-
(3n+2)×(-
)n(14分)
| 3 |
| 2 |
a1+a1q+a1q2=
| 9 |
| 2 |
∴
| 1+q |
| q2 |
∴q=1或q=-
| 1 |
| 2 |
当q=1时,a1=
| 3 |
| 2 |
| 3 |
| 2 |
当q=-
| 1 |
| 2 |
| 1 |
| 2 |
所以当q=1时,an=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)当q=1时,Sn=
| 3 |
| 2 |
| 3n(n+1) |
| 4 |
当q=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=6[
1-(-
| ||
1+
|
| 1 |
| 2 |
∴Sn=
| 8 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |

练习册系列答案
相关题目
 +
+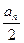 (n∈N+),则其{an}的前10项和为
(n∈N+),则其{an}的前10项和为 的前
的前 项和
项和 .
.