题目内容
【题目】设函数![]()
(1)当a=b=1时,求函数f(x)的图象在点(e2,f(e2))处的切线方程;
(2)当b=1时,若存在![]() ,使f(x1)≤f'(x2)+a成立,求实数a的最小值.
,使f(x1)≤f'(x2)+a成立,求实数a的最小值.
【答案】(1)3x+4y﹣e2=0(2)![]()
【解析】
(1)求![]() ,即可求解;
,即可求解;
(2)存在![]() ,使f(x1)≤f'(x2)+a成立,转化为
,使f(x1)≤f'(x2)+a成立,转化为![]() ,通过配方法求出
,通过配方法求出![]() ,对
,对![]() 分类讨论,确定
分类讨论,确定![]() 的单调性或求出
的单调性或求出![]() 的极小值,进而求出
的极小值,进而求出![]() 的最小值,即可求解.
的最小值,即可求解.
(1)当a=b=1时,f(x)![]() ,
,![]() ,
,
![]() ,f'(e2)
,f'(e2)![]() ,
,
故函数f(x)的图象在点(e2,f(e2))处的切线方程为3x+4y﹣e2=0;
(2)当b=1时,f(x)![]() ,
,
![]() ,
,
设![]()
![]() ,
,
当x∈[e,e2]时,![]() ,g(x)
,g(x)![]() ,
,
故存在![]() ,使
,使![]() 成立,
成立,
只需x∈[e,e2],![]() 即可,下面求f(x)的最小值,
即可,下面求f(x)的最小值,
由于![]() ,
,
当a![]() 时,f'(x)≤0,f(x)在[e,e2]递减,
时,f'(x)≤0,f(x)在[e,e2]递减,
![]() ,得
,得![]() ;
;
当![]() 时,x∈[e,e2],
时,x∈[e,e2],
由于![]() ,
,
若﹣a≥0,即f'(x)≥0,f(x)递增,
![]() ,故不成立;
,故不成立;
若﹣a<0,即0<a![]() ,根据复合函数的单调性,
,根据复合函数的单调性,
f'(x)在[e,e2]单调递增,存在唯一零点m∈(e,e2),
f'(m)=0,使得f(x)在[e,m],f'(x)<0,f(x)递减;
f(x)在(m,e2],f'(x)>0,f(x)递增;
故f(x)![]() ,m∈(e,e2),
,m∈(e,e2),
若![]() 成立,即
成立,即![]() 成立,
成立,
设![]() ,x∈(e,e2),
,x∈(e,e2),
![]() 递减,
递减,
所以![]() ,
,
所以不成立;
综上,![]() ,
,
故a的最小值为![]() .
.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】2016年1月1日,我国全面实行二孩政策,某机构进行了街头调查,在所有参与调查的青年男女中,持“响应”“犹豫”和“不响应”态度的人数如表所示:
响应 | 犹豫 | 不响应 | |
男性青年 | 500 | 300 | 200 |
女性青年 | 300 | 200 | 300 |
(1)根据已知条件完成下面的2×2列联表,并判断能否有97.5%的把握认为犹豫与否与性别有关;
犹豫 | 不犹豫 | 总计 | |
男性青年 |
|
|
|
女性青年 |
|
|
|
总计 |
|
| 1800 |
(2)以表中频率作为概率,若从街头随机采访青年男女各2人,求4人中“响应”的人数恰好是“不响应”的人数(“不响应”的人数不为0)的2倍的概率.
参考公式: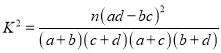
参考数据:
P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |