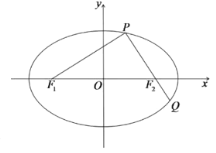
题目内容
【题目】设![]() 是圆
是圆![]() 上的任意一点,
上的任意一点,![]() 是过点
是过点![]() 且与
且与![]() 轴垂直的直线,
轴垂直的直线,![]() 是直线
是直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() .当点
.当点![]() 在圆
在圆![]() 上运动时,记点
上运动时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过
,过![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,交直线
两点,交直线![]() 于点
于点![]() .判定直线
.判定直线![]() 的斜率是否依次构成等差数列?并说明理由.
的斜率是否依次构成等差数列?并说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)设点![]() ,
,![]() ,由条件的线段比例可得
,由条件的线段比例可得![]() ,
,![]() ,代入圆的方程中即可得解;
,代入圆的方程中即可得解;
(2)设直线![]() 的方程为
的方程为![]() ,与椭圆联立得得
,与椭圆联立得得![]() ,设
,设![]() ,
,![]() ,由
,由![]()
![]() ,结合韦达定理代入求解即可.
,结合韦达定理代入求解即可.
(1)设点![]() ,
,![]() ,因为
,因为![]() ,点
,点![]() 在直线
在直线![]() 上,
上,
所以![]() ,
,![]() .①
.①
因为点![]() 在圆
在圆![]() :
:![]() 上运动,所以
上运动,所以![]() .②
.②
将①式代入②式,得曲线![]() 的方程为
的方程为![]() .
.
(2)由题意可知![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() 的坐标为
的坐标为![]() .
.
由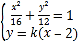 ,得
,得![]() .
.
设![]() ,
,![]() ,则有
,则有![]() ,
,![]() .③
.③
记直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,
,
从而![]() ,
,![]() ,
,![]() .
.
因为直线![]() 的方程为
的方程为![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]()
![]()
![]() .④
.④
把③代入④,得 .
.
又![]() ,所以
,所以![]() ,
,
故直线![]() ,
,![]() ,
,![]() 的斜率成等差数列.
的斜率成等差数列.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
| 12 |
|
|
| |
| 4 |
|
|
| |
合计 |
|
![]() 根据上面图表,求
根据上面图表,求![]() 处的数值
处的数值
![]() 在所给的坐标系中画出
在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
![]() 根据题中信息估计总体平均数,并估计总体落在
根据题中信息估计总体平均数,并估计总体落在![]() 中的概率.
中的概率.