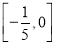题目内容
1.设a1,a2,a3.a4是各项为正数且公差为d(d≠0)的等差数列.(1)证明:2${\;}^{{a}_{1}}$,2${\;}^{{a}_{2}}$,2${\;}^{{a}_{3}}$,2${\;}^{{a}_{4}}$依次构成等比数列;
(2)是否存在a1,d,使得a1,a22,a33,a44依次构成等比数列?并说明理由;
(3)是否存在a1,d及正整数n,k,使得a1n,a2n+k,a3n+2k,a4n+3k依次构成等比数列?并说明理由.
分析 (1)根据等比数列和等差数列的定义即可证明;
(2)利用反证法,假设存在a1,d使得a1,a22,a33,a44依次构成等比数列,推出矛盾,否定假设,得到结论;
(3)利用反证法,假设存在a1,d及正整数n,k,使得a1n,a2n+k,a3n+2k,a4n+3k依次构成等比数列,得到a1n(a1+2d)n+2k=(a1+d)2(n+k),且(a1+d)n+k(a1+3d)n+3k=(a1+2d)2(n+2k),利用等式以及对数的性质化简整理得到ln(1+3t)ln(1+2t)+3ln(1+2t)ln(1+t)=4ln(1+3t)ln(1+t),(**),多次构造函数,多次求导,利用零点存在定理,推出假设不成立.
解答 解:(1)证明:∵$\frac{{2}^{{a}_{n+1}}}{{2}^{{a}_{n}}}$=${2}^{{a}_{n+1}-{a}_{n}}$=2d,(n=1,2,3,)是同一个常数,
∴2${\;}^{{a}_{1}}$,2${\;}^{{a}_{2}}$,2${\;}^{{a}_{3}}$,2${\;}^{{a}_{4}}$依次构成等比数列;
(2)令a1+d=a,则a1,a2,a3,a4分别为a-d,a,a+d,a+2d(a>d,a>-2d,d≠0)
假设存在a1,d使得a1,a22,a33,a44依次构成等比数列,
则a4=(a-d)(a+d)3,且(a+d)6=a2(a+2d)4,
令t=$\frac{d}{a}$,则1=(1-t)(1+t)3,且(1+t)6=(1+2t)4,(-$\frac{1}{2}$<t<1,t≠0),
化简得t3+2t2-2=0(*),且t2=t+1,将t2=t+1代入(*)式,
t(t+1)+2(t+1)-2=t2+3t=t+1+3t=4t+1=0,则t=-$\frac{1}{4}$,
显然t=-$\frac{1}{4}$不是上面方程的解,矛盾,所以假设不成立,
因此不存在a1,d,使得a1,a22,a33,a44依次构成等比数列.
(3)假设存在a1,d及正整数n,k,使得a1n,a2n+k,a3n+2k,a4n+3k依次构成等比数列,
则a1n(a1+2d)n+2k=(a1+d)2(n+k),且(a1+d)n+k(a1+3d)n+3k=(a1+2d)2(n+2k),
分别在两个等式的两边同除以a12(n+k),a12(n+2k),并令t=$\frac{d}{{a}_{1}}$,(t>$-\frac{1}{3}$,t≠0),
则(1+2t)n+2k=(1+t)2(n+k),且(1+t)n+k(1+3t)n+3k=(1+2t)2(n+2k),
将上述两个等式取对数,得(n+2k)ln(1+2t)=2(n+k)ln(1+t),
且(n+k)ln(1+t)+(n+3k)ln(1+3t)=2(n+2k)ln(1+2t),
化简得,2k[ln(1+2t)-ln(1+t)]=n[2ln(1+t)-ln(1+2t)],
且3k[ln(1+3t)-ln(1+t)]=n[3ln(1+t)-ln(1+3t)],
再将这两式相除,化简得,
ln(1+3t)ln(1+2t)+3ln(1+2t)ln(1+t)=4ln(1+3t)ln(1+t),(**)
令g(t)=4ln(1+3t)ln(1+t)-ln(1+3t)ln(1+2t)+3ln(1+2t)ln(1+t),
则g′(t)=$\frac{2}{(1+t)(1+2t)(1+3t)}$[(1+3t)2ln(1+3t)-3(1+2t)2ln(1+2t)+3(1+t)2ln(1+t)],
令φ(t)=(1+3t)2ln(1+3t)-3(1+2t)2ln(1+2t)+3(1+t)2ln(1+t),
则φ′(t)=6[(1+3t)ln(1+3t)-2(1+2t)ln(1+2t)+3(1+t)ln(1+t)],
令φ1(t)=φ′(t),则φ1′(t)=6[3ln(1+3t)-4ln(1+2t)+ln(1+t)],
令φ2(t)=φ1′(t),则φ2′(t)=$\frac{12}{(1+t)(1+2t)(1+3t)}$>0,
由g(0)=φ(0)=φ1(0)=φ2(0)=0,φ2′(t)>0,
知g(t),φ(t),φ1(t),φ2(t)在(-$\frac{1}{3}$,0)和(0,+∞)上均单调,
故g(t)只有唯一的零点t=0,即方程(**)只有唯一解t=0,故假设不成立,
所以不存在a1,d及正整数n,k,使得a1n,a2n+k,a3n+2k,a4n+3k依次构成等比数列.
点评 本题主要考查等差数列、等比数列的定义和性质,函数与方程等基础知识,考查代数推理、转化与化归及综合运用数学知识探究与解决问题的能力,属于难题.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案| A. | 0<x1x2<1 | B. | x1x2=1 | C. | 1<x1x2<2 | D. | x1x2≥2 |
 设X~N(μ1,σ12),Y~N(μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是( )
设X~N(μ1,σ12),Y~N(μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是( )| A. | P(Y≥μ2)≥P(Y≥μ1) | B. | P(X≤σ2)≤P(X≤σ1) | ||
| C. | 对任意正数t,P(X≤t)≥P(Y≤t) | D. | 对任意正数t,P(X≥t)≥P(Y≥t) |
 中,
中,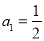 ,
,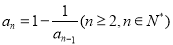 .
.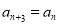 ;
;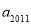 .
. ,
, ,
, ,
, ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
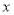 ,
, 满足不等式组
满足不等式组 时,
时,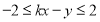 恒成立,则实数
恒成立,则实数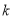 的取值范围是( )
的取值范围是( ) B.
B.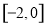
 D.
D.