题目内容
(本小题满分12分)
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(1)完成下面的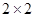 列联表;
列联表;
| | 不喜欢运动 | 喜欢运动 | 合计 |
| 女生 | 50 | | |
| 男生 | | | |
| 合计 | | 100 | 200 |
 和
和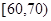 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.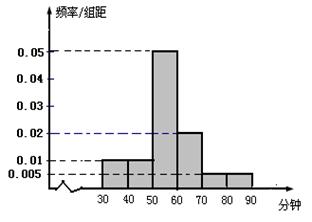
(1)列联表详见解析;(2)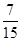 .
.
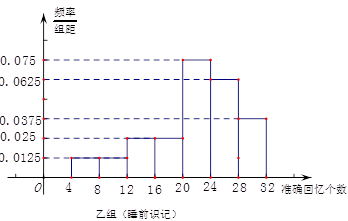
解析试题分析:(1)利用分层抽样填表;(2)利用频率分步直方图求出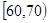 内的人数和在
内的人数和在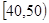 的人数,列出所有的情况,列出概率.
的人数,列出所有的情况,列出概率.
试题解析:(1)根据分层抽样的定义,知抽取男生130人,女生70人, 1分
3分 不喜欢运动 喜欢运动 合计 女生 50 20 70 男生 50 80 130 合计 100 100 200
(2)由直方图知在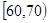 内的人数为4人,设为
内的人数为4人,设为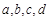 .
.
在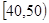 的人数为2人,设为
的人数为2人,设为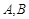 . 5分
. 5分
从这6人中任选2人有AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,ab,ac,ad,bc,bd,cd
共15种情况 7分
若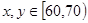 时,有
时,有 共六种情况. 9分
共六种情况. 9分
若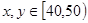 时,有
时,有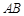 一种情况. 10分
一种情况. 10分
事件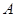 :“她们在同一区间段”所包含的基本事件个数有
:“她们在同一区间段”所包含的基本事件个数有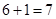 种, 11分
种, 11分
故 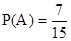
答:两名女生的运动时间在同一区间段的概率为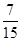 . 12分
. 12分
考点:1.分层抽样;2.频率分步直方图.

 阅读快车系列答案
阅读快车系列答案在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(Ⅰ)根据以上数据建立一个2×2列联表;
(Ⅱ)试判断是否有97.5%的把握认为“休闲方式与性别有关”?
下面临界值表仅供参考:
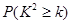 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
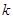 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
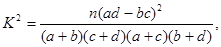 其中
其中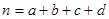 )
) 下表是某单位在2013年1—5月份用水量(单位:百吨)的一组数据:
月份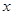 | 1 | 2 | 3 | 4 | 5 |
用水量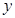 | 4 5 | 4 | 3 | 2 5 | 1 8 |
(Ⅰ)若由线性回归方程得到的预测数据与实际检验数据的误差不超过0 05,视为“预测可靠”,通过公式得
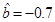 ,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;(Ⅱ)从这5个月中任取2个月的用水量,求所取2个月的用水量之和小于7(单位:百吨)的概率
参考公式:回归直线方程是:
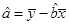 ,
,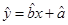
某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了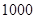 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
结果用二维等高条形图表示,如图.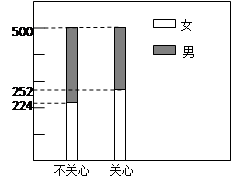
(1)完成列联表,并判断能否有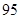 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?
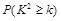 | 0.10 | 0.05 | 0.01 |
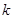 | 2.706 | 3.841 | 6.635 |
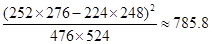
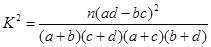 ;
;| | 女 | 男 | 合计 |
| 关心 | | | 500 |
| 不关心 | | | 500 |
| 合计 | | 524 | 1000 |
(2)已知校团委有青年志愿者100名,他们已参加活动的情况记录如下:
| 参加活动次数 | 1 | 2 | 3 |
| 人数 | 10 | 50 | 40 |
(i)从志愿者中任选两名学生,求他们参加活动次数恰好相等的概率;
(ii)从志愿者中任选两名学生,用
 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望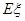 .
. 
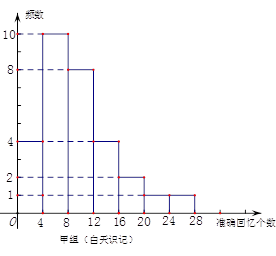
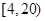 个范围内的学生中随机选2人,求能准确回忆
个范围内的学生中随机选2人,求能准确回忆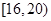 个单词至少有一人的概率.
个单词至少有一人的概率.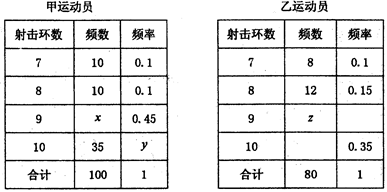
 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求
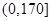 ,第二类在
,第二类在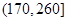 ,第三类在
,第三类在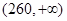 (单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示. 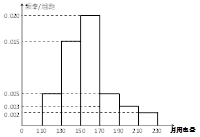
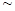 75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
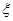 表示抽到PM2.5监测数据超标的天数,求
表示抽到PM2.5监测数据超标的天数,求